Определение количества участков балки.

 

Границами участков являются места расположения тех сечений, где происходит скачкообразное изменение: физико-механических характеристик материала конструкций, формы или размеров, а также внешних нагрузок. Рассматриваемая двухопорная балка имеет постоянное поперечное сечение и четыре участка, обозначенные как: участок I - AB, участок II - BC, участок III - CD, участок IV - DE (рис.10).

3. Составление аналитических выражений внутренних усилий Q_y и M_x.

 

Используем метод сечений. На каждом участке проводим условный разрез в любом месте и берём в рассмотрение одну из двух частей всей балки, ту, к которой приложено меньше нагрузок. Рассматриваем равновесие отсечённой части.

 

Участок AB. 0 £ z ₁ £ 0,6 м.

Рассмотрим равнове­сие левой части балки длиной z ₁ (рис. 12, a). Составим уравнения равновесия всех сил относительно точки сечения о:

 

∑F_y=0 - Q(z₁ ) - R_A=0; Q(z₁)= - R_A= -109,4 кН, (постоянная величина).

 

∑М_о=0 M(z₁ ) - m + R_A∙ z₁=0; M(z₁ )= m - R_A∙ z₁, (уравнение прямой линии).

Подставив в полученное выражение для изгибающего момента значения z ₁ , соответству­ющие граничным сечениям участка AB, определим величины M(z₁), возникающие в этом сечении:

M(0)= m =24 кН∙м; M(0,6)= 24-109,4∙0,6= -41,6 кН∙м.

 

 

 

а) б)

Рис.12

 

а)

 

 

б)

 

 

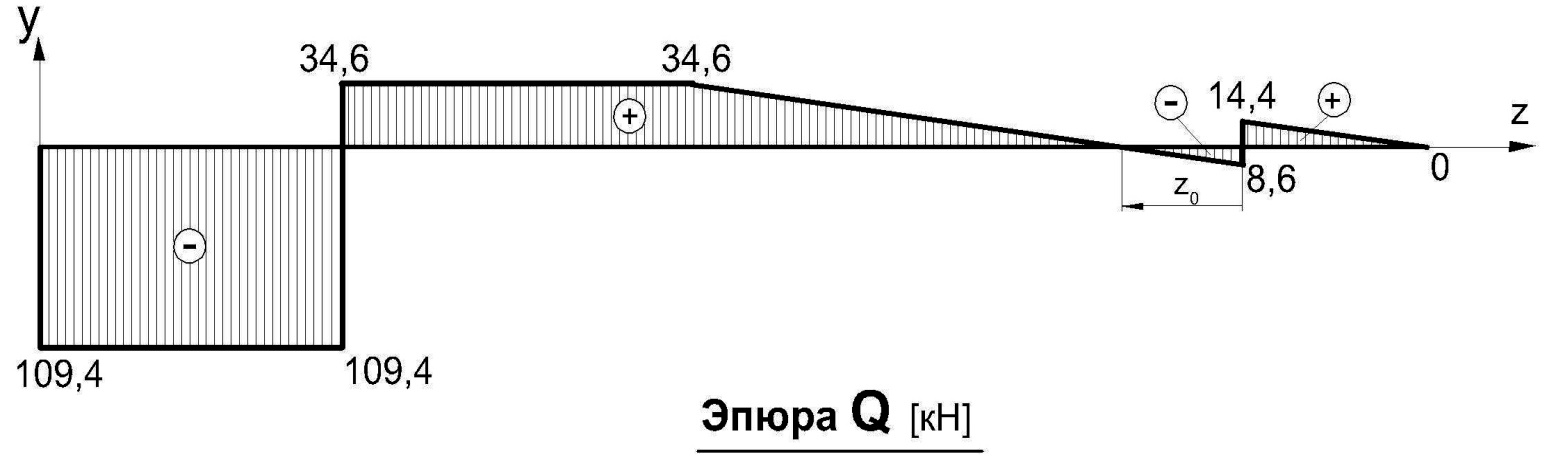
в)

 

 

 

г)

 

Рис.13

 

Участок BC. 0 £ z ₂ £ 0,72 м.

 

Рассмотрим равнове­сие левой части балки длиной z ₂ (рис. 12, б). Составим уравнения равновесия всех сил относительно точки сечения о:

 

∑F_y=0 - Q(z₂)+F - R_A=0; Q(z₂)=F - R_A= 34,6 кН, (постоянная величина).

 

∑М_о=0 M(z₂ ) - m - F∙ z₂ + R_A∙ (z₂+0,6)=0; M(z₂ )= m + F∙ z₂ - R_A∙(z₂+0,6).

Подставив в полученное выражение для изгибающего момента значения z ₂ , соответству­ющие граничным сечениям участка BC, определим величины M(z₂), возникающие в этом сечении:

M(0)= m - R_A∙0,6 = 24-109,4∙0,6 = -41,6 кН∙м.

 

M(0,72)= m + F∙ 0,72 - R_A∙(0,72+0,6)= 24+144∙0,72-109,4∙1,32= -16,7 кН∙м.

Участок DE. 0 £ z ₃ £ 0,36 м.

 

Рассмотрим равнове­сие правой части балки длиной z ₃ (рис. 14, а). Составим уравнения равновесия всех сил относительно точки сечения о:

 

∑F_y=0 Q(z₃ ) - q∙ z₃=0; Q(z₃)= q∙ z₃, (уравнение прямой линии).

 

Подставив в полученное выражение для поперечной силы значения z ₃ , соответству­ющие граничным сечениям участка DE, определим величины Q(z₃), возникающие в этом сечении:

Q(0)= 0; Q(0,36)= 40∙0,36 = 14,4 кН.

 

∑М_о=0 M(z₃ )+q∙ z₃∙ 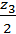=0; M(z₃ )= - q∙ , (уравнение параболы).

Подставив в полученное выражение для изгибающего момента значения z ₃ , соответству­ющие граничным сечениям участка DE, определим величины M(z₃), возникающие в этом сечении:

M(0)= 0; M(0,36)= -2,6 кН∙м.

Участок CD. 0 £ z ₄ £ 1,08 м

 

Рассмотрим равнове­сие правой части балки длиной z ₄ (рис. 14, б). Составим уравнения равновесия всех сил относительно точки сечения о:

 

∑F_y=0 Q(z₄ )+ R_D - q∙(z₄+0,36)=0; Q(z₄)= - R_D + q∙(z₄+0,36),

(уравнение прямой линии).

 

а) б)

Рис.14

 

Подставив в полученное выражение для поперечной силы значения z ₄ , соответству­ющие граничным сечениям участка CD, определим величины Q(z₄),

Q(0)= - R_D + q∙0,36= -23+40∙0,36= -8,6 кН.

Q(1,08)= - R_D + q∙(0,36+1,08)= -23+40∙1,44= 34,6 кН.

 

∑М_о=0 M(z₄ )+q∙(z₄+0,36) ∙ - R_D∙ z₄=0;

M(z₄ )= - q∙ + R_D∙ z₄, (уравнение параболы).

 

Подставив в полученное выражение для изгибающего момента значения z ₄ , соответству­ющие граничным сечениям участка CD, определим величины M(z₄), возникающие в этом сечении:

M(0)= - q ∙ = - 40 ∙ 0,065= -2,6 кН∙м.

 

M(1,08)= - q ∙ + R_D∙ 1,08= - 40 ∙1,04 + 23∙1,08= -16,7 кН∙м.

 

Поперечная сила Q(z₄) на этом участке принимает в некотором сечении нулевое значение и меняет знак при прохож­дении через него (рис. 12, в). Поэтому в сечении, где Q(z₄)= 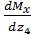= 0, будет экстремальное значение изгибающего момента M(z₄). Для его определения найдем величину z ₀ , при котором Q(z₄) = 0. Приравняв выражение для Q(z₄) к нулю, получим:

Q(z₄)=0; - R_D + q∙(0,36+z₀)=0; z₀= = = 0,22 м.

 

Подставив найденное значение z ₀ = 0,22 м в выражение для M(z₄), найдем величину экстремального значения изгибающего мо­мента M _max на этом участке:

M _max = - q∙ + R_D∙ z₀= - q ∙ 0,17 + 23 ∙ 0,22 = -1,7 кН∙м.

4.Построение эпюр Q_y и M_x для всей балки.

Откладываем перпендикулярно от оси абсцисс в удобном для пользования масштабе значения Q_y и M_x , возникающие в харак­терных и промежуточных сечениях каждого участка. Соединяем концы полученных ординат линиями, соответствующими законам изменения Q_y и M_x на этих участках; строим эпюры Q_y и M_x для всей балки (рис. 13, в,г).