Согласно закону Фарадея, любое изменение магнитного потока через сечение замкнутого контура приводит к возникновению ЭДС индукции в этом контуре. С другой стороны, ток, протекающий по контуру, порождает магнитное поле и обуславливает наличие магнитного потока через сечение этого же контура. В этом случае магнитный поток будет изменяться при изменении тока в контуре. Возникающее индукционное электрическое поле препятствует, по закону Ленца, изменению тока в контуре. Если сила тока увеличивается, индукционное электрическое поле будет замедлять его нарастание; при уменьшении силы тока оно будет поддерживать ток. Можно сказать, что при изменении силы тока в контуре в нем возникает ЭДС индукции, препятствующая этому изменению. Это явление получило название самоиндукции.
Магнитный поток, сцепленный с контуром, зависит не только от силы тока в нем, но и от размеров и формы контура, от магнитных свойств окружающей среды. Однако во всех случаях он пропорционален силе тока, протекающего в контуре, т.е.:
Ф=LI,
где L – коэффициент пропорциональности, называемый индуктивностью контура, зависящий только от геометрических свойств контура и магнитных свойств окружающей среды. Подставляя магнитный поток в формулу для ЭДС индукции, получим:
 .
.
Последнее соотношение справедливо, если индуктивность контура не меняется.
Из приведенной формулы следует, что:
 .
.
Очевидно, что L= 1, если  и скорость изменения тока равны соответствующим единицам. В системе СИ за единицу индуктивности принимают индуктивность такого контура, в котором при скорости изменения тока в 1 А за 1 с возникает ЭДС самоиндукции равной 1 В. Эту единицу именуют Генри (Гн):
и скорость изменения тока равны соответствующим единицам. В системе СИ за единицу индуктивности принимают индуктивность такого контура, в котором при скорости изменения тока в 1 А за 1 с возникает ЭДС самоиндукции равной 1 В. Эту единицу именуют Генри (Гн):
1 Гн=1  .
.
Вычислим индуктивность длинного соленоида. Магнитный поток через сечение контура равен:
 ,
,
где S – площадь сечения витка;
В – индукция магнитного поля соленоида.
Подставляя известное соотношение, получим:
 .
.
Число витков соленоида N можно выразить через плотность намотки n и длину обмотки l: N=nl. Тогда магнитный поток через все витки соленоида будет равен:
 - объем соленоида.
- объем соленоида.
Теперь нетрудно выразить индуктивность соленоида:
 .
.
Энергия магнитного поля
Пусть в контуре с индуктивностью L и течет ток силой  . При отключении источника постоянного тока, ток в цепи исчезает не мгновенно и лампочка, включенная параллельно индуктивности, продолжает некоторое время гореть. Откуда берется энергия, выделяющаяся в лампочке после отключения источника? Очевидно, что это энергия
. При отключении источника постоянного тока, ток в цепи исчезает не мгновенно и лампочка, включенная параллельно индуктивности, продолжает некоторое время гореть. Откуда берется энергия, выделяющаяся в лампочке после отключения источника? Очевидно, что это энергия  магнитного поля, связанного с контуром. Для ее вычисления достаточно вычислить работу, совершенную током после отключения источника.
магнитного поля, связанного с контуром. Для ее вычисления достаточно вычислить работу, совершенную током после отключения источника.
За время dt током совершается следующая работа:
 .
.
В данном случае мы использовали выражение для ЭДС самоиндукции. Заметим также, что работа положительна, т.к. изменение тока отрицательно. Полная работа при убывании тока от  до 0 может быть вычислена интегрированием:
до 0 может быть вычислена интегрированием:
 .
.
Т.к., как было сказано, работа совершается за счет энергии магнитного поля, то:
 =
=  .
.
Подставляя выражение индуктивности  и исключая ток при помощи выражения для магнитной индукции
и исключая ток при помощи выражения для магнитной индукции  , получим формулу расчета энергии магнитного поля соленоида:
, получим формулу расчета энергии магнитного поля соленоида:
 .
.
Видим, что энергия магнитного поля соленоида пропорциональна объему соленоида, в котором и сосредоточено это поле. Плотность энергии магнитного поля  , т.е. энергия, приходящаяся на единицу объема, равна:
, т.е. энергия, приходящаяся на единицу объема, равна:
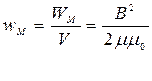 .
.
Полученная формула справедлива не только для соленоида, но может использоваться во всех случаях.
Примеры решения задач
Задача 1
Четыре одинаковых положительных заряда расположены в вершинах квадрата со стороной, равной L. Определить силу действующую на каждый заряд.
Решение



 4
4


 1
1






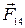


3 2
 |
Рис.1.1
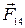
Рис.1.2
Дано:
  L
L
| Решение:
На каждый заряд действуют три силы со стороны трех других. Силы, действующие на первый заряд, изображены на рис.1.1. Из симметрии ясно, что суммарная сила действует по диагонали, в направлении силы  .
По закону Кулона, .
По закону Кулона,  ; ;  .
Вектор .
Вектор  направлен вдоль диагонали квадрата и его длина может быть найдена по теореме Пифагора: направлен вдоль диагонали квадрата и его длина может быть найдена по теореме Пифагора:
 . Окончательно складывая все силы, получим: . Окончательно складывая все силы, получим: 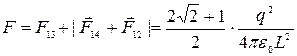 . .
|
| F=? |
Задача 2
Элемент с ЭДС  и внутренним сопротивлением r замкнут на внешнее сопротивление R. Наибольшая мощность, выделяющаяся во внешней цепи, 9 Вт. При этом в цепи течет ток 3 А. Найти ЭДС и внутреннее сопротивление элемента.
и внутренним сопротивлением r замкнут на внешнее сопротивление R. Наибольшая мощность, выделяющаяся во внешней цепи, 9 Вт. При этом в цепи течет ток 3 А. Найти ЭДС и внутреннее сопротивление элемента.
Решение.
Дано:
  Вт Вт
 I=3 А I=3 А
|
Мощность, выделяющаяся в нагрузке, определяется по формуле   , а поскольку она максимальна, то R=r. Следовательно: , а поскольку она максимальна, то R=r. Следовательно:
 Ом. С другой стороны по закону Ома: Ом. С другой стороны по закону Ома:
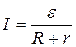 , откуда , откуда  В. В.
|
 =?; r=? =?; r=?
|
Задача 3
Найти внутреннее сопротивление и ЭДС источника тока, если при силе тока 30 А мощность во внешней цепи равна 180 Вт, а при силе тока 10 А эта мощность равна 100 Вт.
| Дано: | Решение: | |
 = 30 A,
P 1 = 180 Вт, = 30 A,
P 1 = 180 Вт,
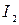 = 10 A P 2 = 100 Вт
_____________
e =?, r =? = 10 A P 2 = 100 Вт
_____________
e =?, r =?
| e = I(r + R) P = IU = I2R e = I1r + P1/I1 e = I2r + P2/I2 | r = (P2/I2 - P1/I1)/(I1 - I2) r = (10 - 6)/20 = 0,2 Ом e = I1r + P1/I1 e = 30 х 0,2 + 6 = 12 В Ответ: e = 12 В, r = 0,2 Ом |
Варианты домашних зачетных заданий
В предлагаемой ниже таблице приведены варианты зачетной контрольной работы № 3 по изложенной в данном пособии теме. Каждая строчка таблицы содержит номера задач, входящих в вариант задания, номер которого определяется номером строки. Вам следует выбрать вариант с номером, совпадающим с последней цифрой номера вашей зачетной книжки.
Задачи приведены в приложении.
| Номер варианта | Номера задач | |||
| 0.1 | 0.2 | 0.3 | 0.4 | |
| 1.1 | 1.2 | 1.3 | 1.4 | |
| 2.1 | 2.2 | 2.3 | 2.4 | |
| 3.1 | 3.2 | 3.3 | 3.4 | |
| 4.1 | 4.2 | 4.3 | 4.4 | |
| 5.1 | 5.2 | 5.3 | 5.4 | |
| 6.1 | 6.2 | 6.3 | 6.4 | |
| 7.1 | 7.2 | 7.3 | 7.4 | |
| 8.1 | 8.2 | 8.3 | 8.4 | |
| 9.1 | 9.2 | 9.3 | 9.4 |
Задачи, включенные в варианты зачетной контрольной работы № 3
0.1. Два одинаковых металлических шарика заряжены так, что заряд одного из них в 5 раз больше другого. Шарики привели в соприкосновение и раздвинули на прежнее расстояние. Во сколько раз изменилась сила взаимодействия, если шарики были заряжены одноименно?
1.1. Два одинаковых металлических шарика заряжены так, что заряд одного из них в 5 раз больше другого. Шарики привели в соприкосновение и раздвинули на прежнее расстояние. Во сколько раз изменилась сила взаимодействия, если шарики имели противоположные по знаку заряды?
2.1. Точечные заряды 20·10-6 Кл и - 10·10-6 Кл находятся в вакууме на расстоянии 5 см друг от друга. Найти напряженность электростатического поля в точке, удаленной на 3см от первого и на 4см от второго заряда. Сделать чертеж.
3.1. Три отрицательных заряда величиной по 3·10-9 Кл каждый расположены в вершинах равностороннего треугольника. Какой заряд нужно поместить в центре треугольника, чтобы система находилась в равновесии?
4.1. Два шара, диаметр которых 10 см и 16 см, а потенциалы, соответственно, 120 В и 50 В, соединяют проводом. Найти потенциалы шаров после их соединения и заряд, перешедший с одного шара на другой.
5.1. Две параллельные заряженные плоскости, поверхностные плотности заряда которых  и
и  , находятся на расстоянии 0,6 см друг от друга. Определить разность потенциалов между плоскостями.
, находятся на расстоянии 0,6 см друг от друга. Определить разность потенциалов между плоскостями.
6.1. Четыре одинаковые капли ртути, заряженные до потенциала 10 В, сливаются в одну. Определить потенциал образовавшейся капли.
7.1. Два конденсатора емкостью  и
и  соединены последовательно и присоединены к батарее с
соединены последовательно и присоединены к батарее с  В. Определить заряды конденсаторов и разности потенциалов между их обкладками.
В. Определить заряды конденсаторов и разности потенциалов между их обкладками.
8.1. Расстояние между пластинами плоского конденсатора d=2 см, разность потенциалов 600 В. Заряд каждой пластины 40 нКл. Определить энергию W поля конденсатора и силу взаимного притяжения пластин.
9.1.К бесконечной равномерно заряженной вертикальной плоскости подвешен на нити одноименно заряженный шарик массой m= 50 мг и зарядом Q =0,6 нКл. Сила натяжения нити, на которой висит шарик F =0,7мН. Найти поверхностную плотность заряда на плоскости.
0.2. Ток I в проводнике меняется со временем t по уравнению I=4+2t, где I - в Амперах и t - в секундах. Какое количество электричества q проходит через поперечное сечение проводника за время от  =2 с до
=2 с до  =6 с? При каком постоянном токе
=6 с? При каком постоянном токе  через поперечное сечение проводника за то же время проходит такое же количество электричества?
через поперечное сечение проводника за то же время проходит такое же количество электричества?
1.2. Сколько витков нихромовой проволоки диаметром d =1 мм надо навить на фарфоровый цилиндр радиусом a =2,5 см, чтобы получить печь, сопротивлением R =40 Ом?
2.2. Вольфрамовая нить электрической лампочки при  имеет сопротивление
имеет сопротивление  =35,8 Ом. Какова будет температура
=35,8 Ом. Какова будет температура  нити лампочки, если при включении в сеть напряжением U =120 В по нити идет ток I =0,33 А? Температурный коэффициент сопротивления вольфрама a=4,6×
нити лампочки, если при включении в сеть напряжением U =120 В по нити идет ток I =0,33 А? Температурный коэффициент сопротивления вольфрама a=4,6×  .
.
3.2.Два последовательно соединенных элемента с одинаковыми ЭДС 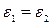 = 2В и внутренними сопротивлениями
= 2В и внутренними сопротивлениями  =1Ом и
=1Ом и  =1,5Ом, замкнуты на внешнее сопротивление R =0,5Ом. Найти разность потенциалов U на зажимах каждого элемента.
=1,5Ом, замкнуты на внешнее сопротивление R =0,5Ом. Найти разность потенциалов U на зажимах каждого элемента.
4.2. Имеется предназначенный для измерения токов до I =15 мA амперметр с сопротивлением  =5 Ом. Какое сопротивление R надо взять и как его подключить, чтобы амперметром можно было измерять: а) ток до 150 мA; б)разность потенциалов до 150 В?
=5 Ом. Какое сопротивление R надо взять и как его подключить, чтобы амперметром можно было измерять: а) ток до 150 мA; б)разность потенциалов до 150 В?
5.2. От генератора с 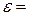 110 В требуется передать энергию на расстояние 250м. Потребляемая мощность 1кВт. Найти минимальное сечение S медных проводов, если потери мощности в сети не должны превышать 1%. Удельное сопротивление меди
110 В требуется передать энергию на расстояние 250м. Потребляемая мощность 1кВт. Найти минимальное сечение S медных проводов, если потери мощности в сети не должны превышать 1%. Удельное сопротивление меди  \=0,017 мкОм × м.
\=0,017 мкОм × м.
6.2. Элемент с ЭДС e=6 В дает максимальный ток 3 A. Найти максимальное количество теплоты, которое может быть выделено во внешнем сопротивлении в единицу времени.
7.2. Электрический чайник, содержащий объем V =600 см  воды при
воды при  , забыли выключить. Сопротивление нагревателя чайника R =16 Ом. Через какое время после включения вода в чайнике выкипит? Напряжение в сети U =120 В, КПД нагревателя 60%, удельная теплоемкость воды 4190Дж/(кг K), удельная теплота парообразования 2,26 М Дж/кг.
, забыли выключить. Сопротивление нагревателя чайника R =16 Ом. Через какое время после включения вода в чайнике выкипит? Напряжение в сети U =120 В, КПД нагревателя 60%, удельная теплоемкость воды 4190Дж/(кг K), удельная теплота парообразования 2,26 М Дж/кг.
8.2 Вольтметр с внутренним сопротивлением R 1 = 150 0м, подключенный к зажимам батареи, показывает U = 30 В. Амперметр с внутренним сопротивлением R 2 = 5 Ом, подключенный к зажимам той же батареи, показывает ток I = 5 А. Найти ток короткого замыкания батареи.
9.2. ЭДС батарейки карманного фонаря 4,5 В, её внутреннее сопротивление 3 0м. Столько таких батареек можно соединить последовательно, чтобы питать лампу, рассчитанную на напряжение 200 В и мощностью 60 Вт?
0.3. ЭДС батареи e=12 В. При силе тока I =4 А, к.п.д. батареи h=0,6. Определить внутреннее сопротивление r батареи.
1.3. Аккумулятор с внутренним сопротивлением r= 0,08 Ом при токе 4 А отдает во внешнюю цепь мощность 8 Вт. Какую мощность отдает аккумулятор во внешнюю цепь при токе 6 А?
2.3. Найти токи  в отдельных ветвях мостика Уитстона при условии, что через гальванометр идет ток
в отдельных ветвях мостика Уитстона при условии, что через гальванометр идет ток 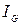 =0. ЭДС элемента e=2 В, сопротивления
=0. ЭДС элемента e=2 В, сопротивления  =30 Ом,
=30 Ом,  =45 Ом и
=45 Ом и  =200 Ом (рис.1.1).
=200 Ом (рис.1.1).











 |
G
 |







 | |||
 | |||
e
Рис.1.1
3.3. Батареи имеют ЭДС  =2 В и
=2 В и 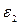 =1 В, сопротивления
=1 В, сопротивления  =1 кОм,
=1 кОм,  =0,5кОм и
=0,5кОм и  =0,2 кОм, сопротивление амперметра
=0,2 кОм, сопротивление амперметра  =0,2 кОм. Найти показание амперметра (рис.1.2).
=0,2 кОм. Найти показание амперметра (рис.1.2).
 |




 А
А







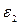





Рис.1.2
4.3. Батареи имеют ЭДС  =2 В и
=2 В и 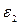 =3 В, сопротивление
=3 В, сопротивление  =1,5кОм, сопротивление амперметра
=1,5кОм, сопротивление амперметра  =0,5кОм. Падение напряжения на сопротивлении
=0,5кОм. Падение напряжения на сопротивлении  равно 1В (ток через
равно 1В (ток через  направлен сверху вниз). Найти показание амперметра (рис.1.2).
направлен сверху вниз). Найти показание амперметра (рис.1.2).
5.3. Батареи имеют ЭДС  =
= 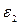 , сопротивления
, сопротивления  =
=  =100Ом, сопротивление вольтметра
=100Ом, сопротивление вольтметра  =150 Ом. Показание вольтметра равно U =150 В. Найти ЭДС батарей (рис.1.3).
=150 Ом. Показание вольтметра равно U =150 В. Найти ЭДС батарей (рис.1.3).
6.3. Батареи имеют ЭДС  =
= 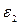 =110В, сопротивления
=110В, сопротивления  =
=  =0,2кОм, сопротивление вольтметра
=0,2кОм, сопротивление вольтметра  =1 кОм. Найти показание вольтметра (рис.1.3).
=1 кОм. Найти показание вольтметра (рис.1.3).




 |







 V
V 

Рис.1.3
7.3. Источник тока имеет сопротивление, сравнимое с сопротивлением вольтметров. Один вольтметр, подключенный к зажимам источника, показал 10 В. Другой вольтметр, присоединённый к источнику вместо первого, показал 15 В. Когда же эти вольтметры соединили последовательно и подключили к зажимам источника, то первый показал 4 В, а второй 12 В. Найти ЭДС источника.
8.3. Найти внутреннее сопротивление источника тока, если известно, что мощность, выделяющаяся во внешней цепи, одинакова при внешних сопротивлениях  Ом и
Ом и  Ом. Определить к.п.д. источника в каждом из этих случаев.
Ом. Определить к.п.д. источника в каждом из этих случаев.
9.3. По ошибке для сети с напряжением 127 В была приобретена спираль, рассчитанная на сеть с напряжением 220 В и мощностью 550 Вт. Какова мощность этой спирали в сети с напряжением 127 В?
0.4. На рис.1.4 изображены сечения трех прямолинейных бесконечно длинных проводников с токами. Расстояния АВ=ВС= 5 см, токи  и
и  . Найти точку на прямой АС, в которой индукция магнитного поля, вызванная этими токами равна нулю.
. Найти точку на прямой АС, в которой индукция магнитного поля, вызванная этими токами равна нулю.





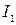


А В С
Рис.1.4
1.4. Решить предыдущую задачу при условии, что токи текут в одном направлении.
2.4. Ток, силой 20 А, протекая по кольцу из медной проволоки сечением S =1,0  , создает в центре кольца напряженность магнитного поля
, создает в центре кольца напряженность магнитного поля  . Какая разность потенциалов приложена к концам проволки, образующей кольцо?
. Какая разность потенциалов приложена к концам проволки, образующей кольцо?
3.4. Бесконечно длинный провод образует круговой виток касательный к проводу. По проводу идет ток 5 А. Найти радиус витка, если напряженность магнитного поля в центре витка  .
.
4.4. Сколько ампер-витков потребуется для того, чтобы внутри соленоида малого диаметра и длиной 30 см объемная плотность энергии магнитного поля была равна 1,75 Дж/м  .
.
5.4. Магнитный поток сквозь соленоид без сердечника 5 мкВб. Найти магнитный момент соленоида, если его длина 25см.
6.4. Из проволоки длиной 20 см сделаны квадратный и круговой контуры. Найти вращающие моменты сил, действующие на каждый контур, помещенные в однородное магнитное поле с индукцией 0,1 Тл. По контурам течет ток 2 А. Плоскость каждого контура составляет угол p/3 с направлением магнитного поля.
7.4. Электрон, ускоренный разностью потенциалов 6 кВ, влетает в однородное магнитное поле под углом  к направлению поля. Индукция магнитного поля
к направлению поля. Индукция магнитного поля  мТл. Найти радиус и шаг винтовой траектории.
мТл. Найти радиус и шаг винтовой траектории.
8.4. В однородном магнитном поле, индукция которого  Тл, равномерно вращается рамка с угловой скоростью
Тл, равномерно вращается рамка с угловой скоростью  рад/с. Площадь рамки 150 см
рад/с. Площадь рамки 150 см  . Ось вращения лежит в плоскости рамки, перпендикулярна направлению магнитного поля. Найти максимальную ЭДС индукции во вращающейся рамке.
. Ось вращения лежит в плоскости рамки, перпендикулярна направлению магнитного поля. Найти максимальную ЭДС индукции во вращающейся рамке.
9.4. Обмотка соленоида состоит из N витков медной проволоки, поперечное сечение которой 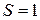 мм
мм  . Длина соленоида 25 см, его электрическое сопротивление 0,2 Ом. Найти индуктивность L соленоида.
. Длина соленоида 25 см, его электрическое сопротивление 0,2 Ом. Найти индуктивность L соленоида.
Литература
Волькенштейн, В.С. Сборник задач по общему курсу физики/В.С. Волькенштейн. – М.: Наука, 1990. – 400 с.
Савельев, И.В. Курс общей физики. т. 2/И.В. Савельев. – М.: Наука, 1982. – 432 с.
Содержание
ВВЕДЕНИЕ. 3
ЭЛЕКТРОСТАТИКА.. 3
§ 1. Электрический заряд. 3
§ 2. Закон Кулона. 4
§ 3. Электростатическое поле. 5
§ 4. Поток вектора  .. 6
.. 6
§ 5. Теорема Остроградского - Гаусса и ее применение для расчета электростатических полей. 7
§ 6. Потенциал. 9
§ 7. Электрическая емкость проводников. 12
§ 8. Энергия электрического поля. 14
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК.. 15
§ 1. Сила и плотность тока. 15
§ 2. Закон Ома для участка цепи. 16
§ 3. Закон Джоуля - Ленца. 17
§ 4. Источники тока. Закон Ома для замкнутой неразветвленной цепи. 18
§ 5. Энергетические характеристики замкнутой цепи. КПД источника. 20
§ 6. Правила Кирхгофа. 22
МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА.. 24
§ 1. Действие магнитного поля на ток. Индукция магнитного поля. 24
§ 2. Принцип суперпозиции для магнитного поля. 26
§ 3. Закон Био-Савара-Лапласа. 26
§ 4. Линии индукции магнитного поля. Циркуляция. 29
§ 5. Взаимодействие параллельных токов. 32
§ 6. Рамка с током в магнитном поле. Магнитный момент. 33
§ 7. Сила Лоренца. Движение заряженных частиц в магнитном поле. 35
§ 8. Работа по перемещению проводника с током в магнитном поле. 37
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ.. 38
§ 1. Закон электромагнитной индукции Фарадея. 38
§ 2. Вывод выражения ЭДС индукции для движущихся проводников. 39
§ 3. Вихревое электрическое поле. 40
§ 4. Явление самоиндукции. Индуктивность. 43
§ 5. Энергия магнитного поля. 44
Примеры решения задач. 45
Варианты домашних зачетных заданий. 47
Задачи, включенные в варианты зачетной контрольной работы № 3. 48
Литература……………………………………………………………………… 53






