Если в пространстве есть магнитное поле с индукцией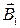 
, создаваемое, например постоянным магнитом, то сила, действующая на какой-либо проводник с током, будет определяться законом Ампера. Если вы поднесете к проводнику второй магнит, создающий поле 
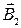, то магнитная сила, действующая на проводник, изменится. Поскольку проводник и ток в нем остались прежними, следовательно, изменилось магнитное поле в месте расположения проводника. На опыте можно установить, что сила действия двух магнитов 
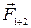равна векторной сумме сил 
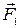и 
, с которыми действует на элемент тока каждый из магнитов. Используя закон Ампера и свойства векторного произведения, это можно записать в виде:
.
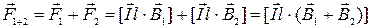С другой стороны, поскольку сила Ампера определяется вектором магнитной индукции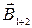 
, имеющимся в пространстве, можно записать:
.
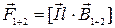Сравнивая два последних выражения, приходим к выводу, что суммарный вектор магнитной индукции равен векторной сумме индукции магнитных полей, создаваемых каждым магнитом в отсутствии другого:
.
Сказанное справедливо не только для двух источников магнитных полей, но и для произвольного их числа. Принцип суперпозиции говорит о независимом наложении магнитных полей.
Закон Био-Савара-Лапласа
На опыте наблюдается не только взаимодействие между постоянным магнитом и проводником с током, но и между двумя проводниками с током в отсутствие магнита. Можно объяснить наличие силы, действующей на первый проводник, тем, что другой проводник с током окружен своим собственным магнитным полем, которое действует на первый проводник по закону Ампера. Таким образом, можно сделать вывод, что вокруг всякого проводника с током образуется магнитное поле. Определить индукцию магнитного поля проводника с током можно при помощи закона Био – Савара – Лапласа, являющегося обобщением опытных фактов.
Удобно сформулировать закон генерации магнитного поля для бесконечно малого элемента тока (длиной dl). Тогда, в соответствие с принципом суперпозиции, индукция любого проводника с током может быть найдена в любой точке наблюдения как векторная сумма полей, создаваемых всеми элементами тока, из которых состоит проводник.
На рис.3.1 изображен элемент тока. Вектор 
соединяет элемент тока и точку наблюдения. Индукцию магнитного поля, создаваемую бесконечно малым элементом тока в точке наблюдения, обозначим как 
:
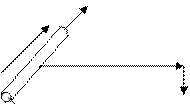
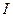
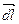
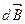
Рис.3.1
где – элементарное магнитное поле, создаваемое элементарным отрезком провода с током I.
Закон Био – Савара – Лапласа в векторной форме, используя систему Си, можно записать в виде:
.
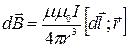В данной форме закон определяет и величину и направление магнитного поля. Видим, что магнитное поле пропорционально величине элемента тока и направлено перпендикулярно и элементу тока и вектору . Здесь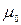 
- магнитная постоянная, равная 
Тл×м/А. Величина 
, учитывающая влияние среды, в которой возникает магнитное, называется относительной магнитной проницаемостью. показывает, во сколько раз в данной среде индукция магнитного поля больше, чем было бы при тех же условиях в вакууме.
Для модуля индукции магнитного поля можно записать следующую формулу:
,
где a - угол между векторами 
.
Видим, что магнитное поле убывает обратно пропорционально квадрату расстояния до точки наблюдения и существенно зависит от направления на точку наблюдения. В частности, электрический ток не создает магнитного поля в точках, лежащих на прямой, совпадающей с направлением тока (a= 0).
Кроме индукции для описания магнитного поля используют напряженность магнитного поля H, в изотропной среде связанную с индукцией по формуле:
.
На напряженность магнитного поля не оказывает влияния окружающая среда. Она определяется только макроскопическими токами.
