Предположим, имеется прямоугольная рамка из проволоки, которая может вращаться относительно вертикальной оси, лежащей в плоскости рамки, а однородное магнитное поле - горизонтально. Если по рамке пропускать ток I, на проводникирамки будут действовать силы Ампера. Поскольку токи в параллельных сторонах рамки имеют противоположные направления, а длины и магнитные поля одинаковы, ясно, что силы, действующие на противоположные стороны, в сумме дают 0. Следовательно, равнодействующая всех сил, действующих на рамку, равна нулю. Это же справедливо и для рамки произвольной формы. В то же время на рамку с током в магнитном поле действует вращающий момент.
Положение рамки, как и любого витка с током, принято характеризовать единичным вектором нормали 
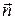к плоскости витка. Если угол между вектором нормали и магнитным полем равен a, то силы, действующие на горизонтальные стороны рамки (длиной 
), равны 
. Эти силы имеют вертикальные направления и не создают вращающего момента относительно оси рамки. Силы, действующие на вертикальные стороны рамки (длиной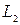 
), равны 
. Плечо каждой из этих сил относительно вертикальной оси равно 
, поэтому суммарный вращающий момент сил, действующих на рамку в магнитном поле равен:
.
Как видим, существуют два положения, при которых вращающий момент обращается в ноль, когда нормаль рамки направлена вдоль или противоположна магнитному полю 
. Это положение равновесия рамки. Одно из этих положения является неустойчивым, а второе устойчивым. Таким образом, можно заключить, что рамка с током, помещенная в однородное магнитное поле, будет поворачиваться, пока не займет устойчивого положения равновесия, в котором плоскость рамки перпендикулярна полю. Аналогично ведет себя в магнитном поле стрелка компаса.
Описанное явление вращения рамки с током в магнитном поле находит практическое применение в электродвигателях и измерительных приборах.
Аналогичным свойством вращения в магнитном поле обладают витки с током независимо от их формы. Ниже мы приведем общие формулы для вращающего момента, справедливые для любых витков.
Вектором магнитного момента называют произведение силы тока в витке на площадь витка и на единичный вектор нормали к витку: 
, причем из двух возможных направлений нормали нужно взять то, при котором из конца вектора 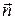ток в витке виден текущим против часовой стрелки. Из сказанного ясно, что вектор магнитного момента витка направлен по нормали к витку.
Величина магнитного момента рамки с током, рассмотренной выше, равна 
.
Используя понятие магнитного момента, выражение для вращающего момента, действующего на виток с током в однородном магнитном поле, удобно записать в следующем виде:
.
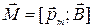Эта формула определяет и величину момента, и ось вращения витка в магнитном поле. В частном случае прямоугольной рамки с током эта формула соответствует величине момента сил, полученной в начале параграфа, а направление момента показано на рис.6.1.
 |
 | |||
 | |||
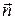I a
Рис. 6.1
