В предыдущем параграфе мы убедились, что явление возникновения индукционных токов в движущихся проводниках не вызывает вопросов. Здесь все согласуется с известными законами физики. Тем не менее, остается неясным причина возникновения индукционного тока в случае неподвижных зарядов.
Вот пример эксперимента. Если взять проводник в виде круглого кольца и «включать» магнитное поле указанного на рис. направления, то индукционный ток возникнет против часовой стрелки.
 | |||
 | |||
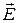
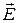
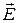
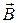
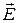
Рис.3.1
Здесь сила Лоренца, связанная с движением электронов вместе с проводником, равна нулю, и, значит, не видно сторонней силы, вызывающей направленное движение электронов вдоль кольца.
Для того, чтобы объяснить возникновение тока в такой ситуации, приходиться предположить, что возникает электрическое поле, направленное по касательной к кольцу в каждой точке (рис.3.1). Поскольку кольцо симметрично, величина напряженности поля должна быть одинаковой в каждой точке кольца. ЭДС индукции, возникающей в кольце, можно выразить через напряженность E, т.к. любая ЭДС равна работе по перемещению единичного заряда. Для кольца радиуса R это дает:
.
Мы получили, что циркуляция поля 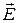по замкнутому контуру не равна нулю, т.е. поле, которое по предположению возникает, должно быть вихревым, а не потенциальным как обычное поле электрических зарядов, циркуляция которого всегда равна нулю.
Таким образом, мы приходим к выводу о необходимости возникновения особого вихревого электрического поля, не связанного с наличием электрических зарядов. Оно должно возникать при изменении магнитного потока через площадь кольца, и его циркуляция должна давать ту же ЭДС индукции, что закон Фарадея. Следовательно, должно выполнятся равенство:
,
где Ф – магнитный поток через кольцо.
С другой стороны, законы природы, конечно, не должны зависеть от формы контура, который мы поместили в магнитное поле. Более того, если быть последовательным, приходится признать, что возникновение вихревого электрического поля также не должно зависеть от наличия или отсутствия в этом месте проводника.
Окончательный вывод можно сформулировать следующим образом: при всяком изменении магнитного поля в окружающем пространстве со временем возникает индукционное вихревое электрическое поле. Если в пространстве присутствует замкнутый проводящий контур, индукционное электрическое поле вызывает в нем индукционный ток.
Пользуясь понятием вихревого электрического поля, закон Фарадея можно сформулировать следующим образом: циркуляция индукционного электрического поля по произвольному замкнутому контуру равна скорости изменения магнитного потока через площадь, ограниченную данным контуром. Сказанное можно выразить в виде равенства:
,
где L – произвольный замкнутый контур;
S – ограниченная им поверхность.
Это уравнение системы Максвелла, позволяющее рассчитать электрические и магнитные поля в любых ситуациях. Написанное интегральное соотношение полностью определяет величину и направление вихревого электрического поля. Оно аналогично закону о циркуляции магнитного поля, о котором шла речь ранее:
.
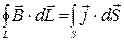Из аналогии уравнений ясно, что силовые линии вихревого электрического поля имеют такое же относительное расположение относительно вызывающего его магнитного поля, какое имеют линии вектора 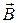относительно вектора плотности тока.
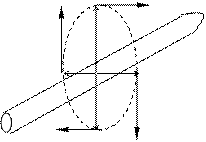
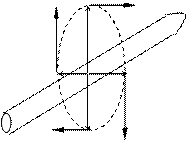
Например, известно, что силовые линии магнитного поля, порождаемого прямолинейным проводником с током, представляют собой окружности, концентрические с осью проводника. Значит, силовые линии вихревого электрического поля соленоида (магнитное поле которого имеет прямые силовые линии) имеют вид окружностей, концентрических с осью соленоида. Указанная аналогия иллюстрируется сопоставлением рис.3.2:
 | |||
 | |||
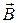
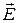
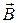
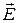
I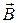
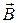
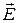
а) б)
Рис.3.2
Второй рисунок соответствует случаю возрастания магнитного поля в соленоиде.
Следует отметить, что вихревое электрическое поле порождается только переменным во времени магнитным полем, а магнитное поле вызывается как переменным, так и постоянным во времени током. В этом состоит отличие вихревого электрического и магнитного полей.
Вихревые электрические поля вызывают в проводящей среде протекание индукционных токов во всем объеме вещества. Нагрев металла вихревыми токами используется в металлургическом производстве в индукционных плавильных печах. В других случаях принимаются меры, чтобы ослабить нагрев материала, вызванный наличием индукционных токов. По этой причине сердечники трансформатора набирают из отдельных пластин.
