Коэффициентом полезного действия источника (КПД) называют отношение мощности, выделяющейся в нагрузке к полной мощности источника.
Для цепи, рассмотренной в предыдущем параграфе, полная мощность источника может быть найдена, если работу источника над единичным зарядом (равную 
) умножить на заряд, протекающий через источник в единицу времени (равный I):
.
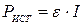Очевидно, что полная мощность источника не является постоянной для данного источника величиной, а зависит от параметров цепи.
Поскольку источник предназначен для создания тока в нагрузке, полезной мощностью называют мощность, выделяющуюся в нагрузке:
.
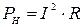Таким образом, для КПД (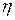
) источника можно получить следующее выражение:
.
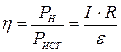Проанализируем зависимость КПД от характеристик электрической цепи. Для рассматриваемой цепи существует связь между силой тока и параметрами элементов, включенных в цепь (закон Ома):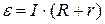 
. Причем для данного источника значения ЭДС и внутреннего сопротивления являются фиксированными. Оставшиеся две величины – сила тока I и сопротивление нагрузки R –могут быть связаны между собой. Возьмем в качестве основной величины сопротивление нагрузки, а силу тока исключим из полученных соотношений при помощи закона Ома. В результате получим:
,
,
.
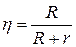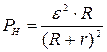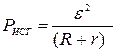КПД равен нулю при R=0, а затем монотонно возрастает, стремясь к единице при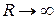 
. Заметим, однако, что КПД, равный 1, соответствует отсутствию тока в цепи (I=0, согласно закону Ома при 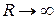). Этот случай соответствует полному отсутствию работы источника, полной и полезной.
Мощность источника имеет максимальное значение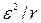 
при R=0 (короткое замыкание), когда 
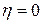. С увеличением сопротивления нагрузки 
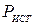монотонно убывает до нуля (бесконечное сопротивление нагрузки и отсутствие тока в цепи).
Более сложная зависимость от сопротивления нагрузки соответствует полезной мощности. При R>r можно пренебречь величиной r в знаменателе выражения для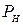 
и убедиться, что она убывает с ростом сопротивления нагрузки. С другой стороны, при R=0, полезная мощность равна нулю. Т.к. мощность всегда положительна, то при промежуточных значениях R она достигает максимального значения. В точке максимума производная функции 
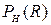обращается в ноль. Вычислив эту производную и приравняв ее нулю, найдем, что точка максимума соответствует R=r. Значит, полезная мощность максимальна, когда сопротивление нагрузки равно внутреннему сопротивлению источника. Значение максимальной полезной мощности получим из общего выражения, положив в нем R=r:
.
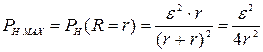Нетрудно также получить, что при этом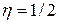 
, т.е. полная мощность источника в этом случае в два раза больше полезной.
Таким образом видим, что максимальная мощность источника достигается при полезной мощности равной нулю, а максимальная полезная мощность – при КПД, равном 1/2, и мощности источника, равной половине максимальной.
Правила Кирхгофа
Каким образом получить уравнения связи между отдельными характеристиками в сложных (разветвленных) цепях, состоящих из нескольких источников и потребителей электроэнергии? Эту задачу можно решить для любой цепи постоянного тока при помощи правил Кирхгофа. Определим некоторые термины.
Узел – точка, к которой присоединено больше двух проводов. Ветвь – участок цепи, на котором нет узлов. Контур – замкнутая часть цепи.
1-й закон Кирхгофа:
