1. Находим область определения функции (если есть точки разрыва, то находим односторонние пределы в этих точках).
2. Проверяем, является ли функция четной, нечетной или общего вида.
3. Находим точки пересечения графика функции с осями координат.
4. Находим асимптоты.
5. Определяем промежутки монотонности и экстремумы.
6. Определяем выпуклость графика функции и точки перегиба.
7. Строим график.
Пример. Исследовать функцию 
.
¦
1. Находим область определения функции.
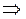
– точка разрыва
2. Определяем четность или нечетность функции.
Функция - общего вида, так как ее область определения несимметрична относительно начала координат.
3.Находим точки пересечения с осями координат.
с осью 
: 
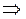точек пересечения нет;
с осью 
: 
.
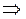
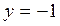4. Находим асимптоты графика функции.
1) - это вертикальная асимптота.
2) При 
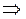горизонтальных асимптот нет
3) 
, 
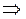
– это наклонная асимптота.
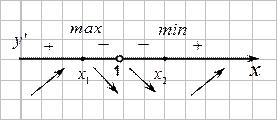5. Находим промежутки монотонности и экстремумы функции. 
. 
при 
, 
.
Критические точки и точку разрыва функции отмечаем на числовой прямой.
– это точка максимума функции,
– это точка минимума функции.
,
.
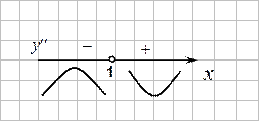6. Находим промежутки выпуклости и точки перегиба графика функции. 
, 
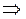на прямой отмечаем только точку разрыва функции
7.Строим график функции.
Наибольшее и наименьшее значение функции на отрезке
Пусть функция 
определена и дифференцируема на отрезке 
. Она может достигать своего наибольшего и наименьшего значения на отрезке в точках экстремума, принадлежащих этому отрезку или на концах отрезка: в точках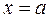 
и 
.
План исследования.
1. Находим точки, принадлежащие отрезку , в которых 
.
2. Находим значения функции в выбранных точках и на концах отрезка.
3. Выбираем самое наибольшее и самое наименьшее значения функции.
Они обозначаются так: 
и 
.
Пример. Найти наибольшее и наименьшее значения функции
на отрезке 
.¦
1. Находим точки, принадлежащие отрезку 
, в которых .
2. Находим значения функции в выбранных точках и на концах отрезка.
; 
; 
.
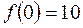3. Выбираем самое наибольшее и самое наименьшее значения функции.
Ответ: 
и 
. ?
ЛИТЕРАТУРА
1. Бугров Я. С., Никольский С. М.“Дифференциальное и интегральное исчисление.”, М., Наука, 1980 г.
2. Видякин В.В., Шабанова М.В. Математический анализ, том 1.: Архангельск, 2002. - 497 с.
3. Данко П.Е. Высшая математика в упражнениях и задачах [Текст]: Учебное пособие в 2-х ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова, 2005. – 404с.
4. Руководство к решению задач по высшей математике [Текст]: Учебное пособие в 2-х ч. Ч.1 /Е.И.Гурский, В.П.Домашов, В.К.Кравцов, А.П.Сильванович; Под общ. Ред. Е.И.Гурского, 1989. – 349 с.
5. Сборник задач по математике для втузов. В 4-х ч [Текст]: Учебное пособие для втузов. Ч.2 / Ред. А.В.Ефимов, Ред. А.С.Поспелов, 2003. – 432с.
6. Шипачев В.С. Основы высшей математики [Текст]: Учебное пособие / В.С.Шипачев, 2002. - 479с.
