1. Теорема Ферма. (Ферма Пьер (1601–1665гг.) – французский математик).
Пусть функция  определена на интервале
определена на интервале  ; в некоторой точке
; в некоторой точке  этого интервала она принимает наибольшее или наименьшее значение.
этого интервала она принимает наибольшее или наименьшее значение.
Тогда, если в точке  существует конечная производная, то она равна нулю, т.е.
существует конечная производная, то она равна нулю, т.е.  .
.
Геометрический смысл теоремы Ферма.


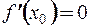
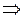

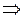 касательная параллельна оси
касательная параллельна оси  .
.
2. Теорема Ролля. (Ролль Мишель (1652–1719гг.) – французский математик)
Пусть функция  определена на
определена на 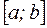 ,
,
причем: 1)  непрерывна на
непрерывна на 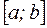 ;
;
2)  дифференцируема на
дифференцируема на  ;
;
3)  .
.
Тогда существует точка  , в которой
, в которой 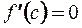 .
.
Геометрический смысл теоремы Ролля.



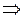

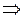 касательная параллельна оси
касательная параллельна оси  .
.
3. Теорема Лагранжа. (Лагранж Жозеф-Луи (1736–1813гг.) – французский математик).
Пусть функция  определена на
определена на 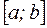 ,
,
причем: 1)  непрерывна на
непрерывна на 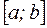 ;
;
2)  дифференцируема на
дифференцируема на  ;
;
Тогда существует такая точка  , что справедлива формула
, что справедлива формула
 .
.
Доказательство. Введем вспомогательную функцию
 .
.
Тогда: 1) 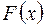 непрерывна на
непрерывна на 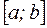 , так как является разностью непрерывной функции
, так как является разностью непрерывной функции  и линейной
и линейной  ;
;
2) 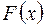 дифференцируема на
дифференцируема на  , т.е. внутри
, т.е. внутри 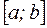 имеет производную
имеет производную  ;
;
3) 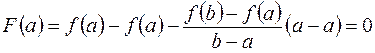 ;
;
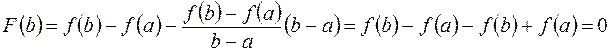
Следовательно, по теореме Ролля существует точка  , в которой
, в которой  , т.е.
, т.е. 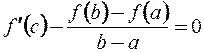
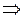
 . ¢
. ¢
Геометрический смысл теоремы Лагранжа.

 – это угловой коэффициент секущей, проходящей через точки
– это угловой коэффициент секущей, проходящей через точки 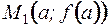 и
и 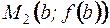 кривой
кривой  ;
;
 – это угловой коэффициент касательной к кривой
– это угловой коэффициент касательной к кривой  в точке с координатами
в точке с координатами  .
.
Таким образом, существует такая точка, в которой касательная параллельна секущей. Таких точек может быть и несколько, но
обязательно одна существует.
Замечание. Равенство  , где
, где  называют формулой Лагранжа, или формулой конечных приращений.
называют формулой Лагранжа, или формулой конечных приращений.
4. Теорема Коши. (Коши Огюстен Луи (1789–1853гг.) – французский математик).
Пусть функции  и
и 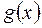 непрерывны на
непрерывны на 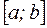 и дифференцируемы на
и дифференцируемы на  . Пусть
. Пусть  .
.
Тогда существует такая точка  , что справедлива формула
, что справедлива формула
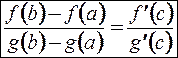 .
.
Эта формула называется формулой Коши, или обобщенной формулой конечных приращений.
Замечание. Для всех четырех теорем указанные в формулировке условия существенны. Если хотя бы одно из них не выполняется, то теоремы не справедливы.
 Например,
Например, 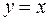 на
на  непрерывна, дифференцируема, но так как
непрерывна, дифференцируема, но так как  и
и 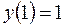 , то теорема Ролля не выполняется, т.е. нет такой точки
, то теорема Ролля не выполняется, т.е. нет такой точки  , где
, где  .
.
Пример. Проверить справедливость теоремы Ролля для функции  на
на  и найти
и найти  .
.
¦  ,
, 
 ,
,  ,
, 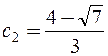 . ?
. ?
Правило Лопиталя
Теорема Лопиталя
(Лопиталь Гильон Франсуа (1661–1704) – французский математик).
Теорема. Пусть функции  и
и 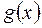 определены и дифференцируемы в некоторой окрестности точки
определены и дифференцируемы в некоторой окрестности точки  , но в самой точке
, но в самой точке  могут быть и не определены. Пусть
могут быть и не определены. Пусть  и
и  в указанной окрестности точки
в указанной окрестности точки  .
.
Тогда, если существует предел 
(конечный или бесконечный), то существует и предел  , причем справедлива формула
, причем справедлива формула  .
.
Эту теорему называют правилом Лопиталя.
Правило Лопиталя раскрывает неопределенность  .
.
Замечания.
1. Правило Лопиталя имеет место и в случаях, когда 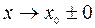 и
и  .
.
2. Правило Лопиталя можно применять и при раскрытии неопределенностей  .
.
3. Если отношение производных приводит к неопределенностям  и
и  , то правило Лопиталя можно применять повторно.
, то правило Лопиталя можно применять повторно.
Пример 1. 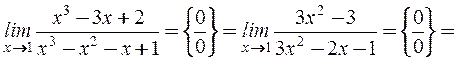
 .
.
Пример 2.  .
.




