В некоторых случаях для нахождения производной сначала можно функцию прологарифмировать, а затем от полученного выражения вычислить производную.
Такая операция называется логарифмическим дифференцированием.
Существуют функции, производные от которых находят лишь с помощью логарифмического дифференцирования.
К таким функциям относится показательно-степенная функция 
.
Прологарифмируем выражение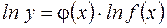 
.
Найдем производную от обеих частей полученного равенства, учитывая, что 
является функцией от 
.
Тогда 
или 
.
Пример 1. Найти производную функции 
.
¦ Прологарифмируем выражение: 
Тогда 
или 
. ?
Пример 2. Найти производную функции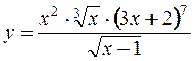 
.
¦ Прологарифмируем выражение:
Тогда 
или
. ?
Производные высших порядков
Производная 
от функции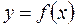 
есть также функция от 
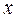и называется производной первого порядка.
Производная от производной первого порядка называется производной второго порядка и обозначается 
.
Производная от производной (
) -го порядка называется производной 
-го порядка и так далее. Начиная с четвертого порядка, производные обозначаются:
или 
, 
или 
и так далее.
Например: 
, 
, 
, 
, 
.
Физический смысл производной второго порядка.
Если функция 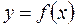описывет закон движения материальной точки по прямой линии, то 
– ускорение точки в момент времени 
.
Производная неявной функции
Пусть функция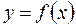 
задана неявно, т.е уравнением 
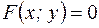, неразрешенным относительно . Чтобы найти производную от по , нужно продифференцировать это уравнение, учитывая, что является функцией от . Затем из полученного выражения выразить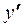 
.
Пример 1. Найти производную 
функции 
.
¦ Найдем производные по от каждой части уравнения.
. ?
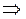
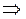
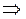
Пример 2. Найти производную второго порядка 
от функции, заданной неявно: 
¦ 1) Найдем 
: 
, 
.
2) Найдем 
: 
, заменим 
. ?
Производная функции, заданной параметрически
Будем говорить, что переменная как функция аргумента 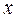задана параметрически, если обе переменные 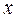и заданы как функции некоторой третьей переменной 
:
, где – параметр (дополнительная переменная).
Предположим, что существуют 
и 
, а функция 
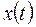имеет обратную функцию 
. Тогда 
.
В этом случае, параметрически заданную функцию можно рассматривать как сложную функцию 
.
Тогда 
.
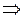
Производная второго порядка находится по формуле:
или 
.
Пример 1. Функция задана параметрически: 
.
Найти производную второго порядка по .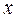
¦ 
. ?
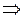
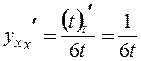Пример 2. Функция задана параметрически: 
.
Найти производную второго порядка по .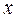
¦ 
. ?
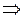
Дифференциал функции
Пусть функция 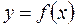имеет отличную от нуля производную
.
Тогда по теореме о связи функции, ее предела и б.м.ф. можно записать 
, где 
при 
.
– это сумма двух б.м.ф. при . При этом первое слагаемое б.м.ф одного порядка с 
, а второе слагаемое б.м.ф более высокого порядка, чем 
.
Поэтому первое слагаемое 
является главной частью приращения функции и называется дифференциалом первого порядка функции 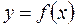в точке .
Обозначают дифференциал так: 
или 
.
Дифференциал равен произведению производной функции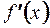 
и приращения аргумента 
. Найдем дифференциал аргумента 
.
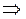
Следовательно, 
.
Геометрический смысл дифференциала первого порядка.
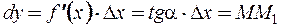
Следовательно, дифференциал первого порядка функции 
в точке –это приращение ординаты касательной, проведенной к графику функции в точке .
Если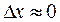 
, то 
. Последнее равенство можно использовать для приближенного вычисления значения 
.
Пример 1. Вычислить 
.
¦ Пусть 
.
Тогда 
?