Пусть функция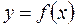 
определена и непрерывна на некотором интервале. Пусть точка 
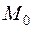на графике функции соответствует значению аргумента 
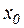, а точка 
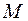– значению 
, где 
– приращение аргумента. Проведем через точк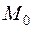и и 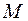прямую и назовем ее секущей.
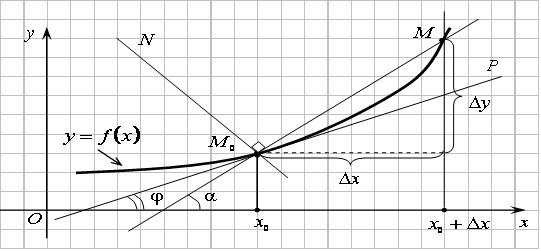
Определение. Касательной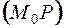 
к графику функции 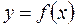в точке 
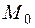называется предельное положение секущей 
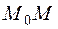при неограниченном приближении точки 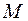по графику к точке 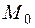(или, что то же самое, при 
).
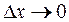Пусть 
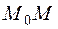– угол между секущей и осью 
, 
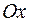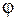– угол между касательной 
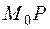и осью .
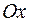На рисунке видно, что угловой коэффициент секущей равен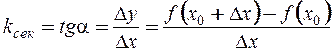 
.
Из определения касательной следует, что угловой коэффициент касательной равен
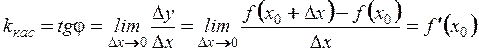
Следовательно, угловой коэффициент касательной, проведенной к графику функции 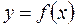в точке с абсциссой 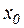, равен значению производной функции в этой точке.
Определение. Прямая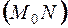 
, перпендикулярная касательной и проходящая через точку касания, называется нормалью к графику функции.
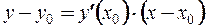– уравнение касательной,
– уравнение нормали,
где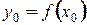 
.
Физический смысл производной
Пусть функция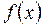 
описывает закон движения материальной точки 
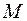по прямой линии, в том смысле, что значение 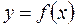- это путь, пройденный точкой за время 
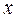. Тогда 
– это мгновенная скорость точки 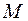в момент времени 
.
Правила дифференцирования функций
И производные элементарных функций
Правила дифференцирования
Пусть функци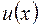и 
и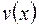 
дифференцируемы.
Тогда:
;
;
;
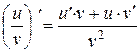Производную сложной функции находим по формуле:
.
11.2. Производные элементарных функций
Используя определение производной, можно показать, что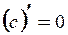 
– производная постоянной функции;
– производная степенной функции.
Выведем производные остальных элементарных функций.
Производные тригонометрических функций.
1. 
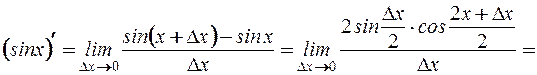
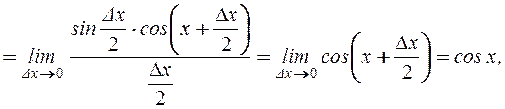
(применили первый замечательный предел)
т.е.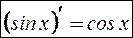 
.
2. 
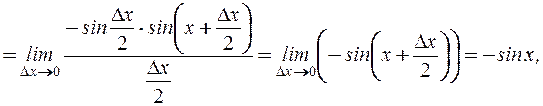
(применили первый замечательный предел)
т.е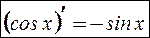 
.
3. 
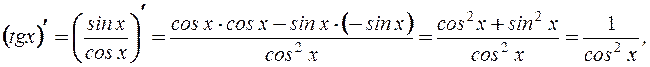
т.е.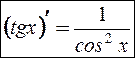 
.
4.
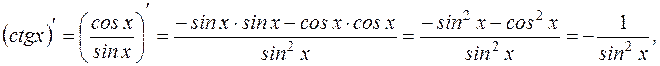т.е.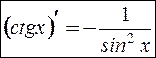 
.
Производная логарифмической функции.
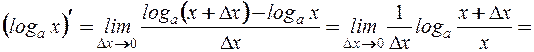
(умножили и разделили на 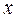) (применили второй замечательный предел)
т.е.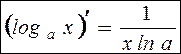 
.
Частный случай: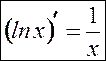 
.
Производная обратной функции. Производная показательной функции.
1. Теорема. Если 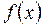в точке имеет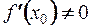 
, то обратная ей функция 
также в точке 
имеет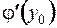 
, причем
.
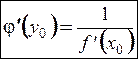2. Показательная функция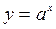 
, обратная ей функция 
.
,
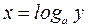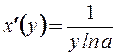
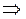
т.е. 
.
Частный случай: 
.
Производные обратных тригонометрических функций.
1. Пусть функция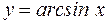 
, где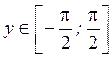 
,
тогда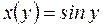 
– обратная ей функция, 
.
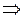
Знак «+» перед корнем, так как функция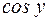 
неотрицательна на отрезке 
.
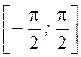Следовательно,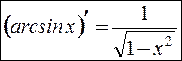 
.
Аналогично получаем: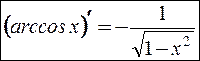 
.
2. Пусть функция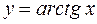 
, где 
,
тогда 
- обратная ей функция,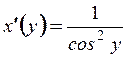 
.
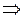
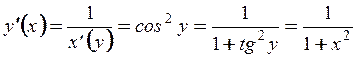Следовательно,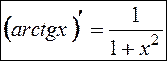 
.
Аналогично получаем: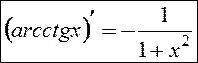 
.
