Первое начало термодинамики

Термодинамическая система, как и любая другая физическая система, состоит из большого ансамбля обособленных частиц. Эти частицы совершают бесконечное тепловое движение и взаимодействуют между собой. Следовательно, внутренняя энергия системы есть сумма всех видов кинетической и потенциальной энергии всех составных частей системы: тел, их молекул, атомов, электронов. Таким образом, в состав внутренней энергии входит кинетическая энергия поступательного и вращательного движений атомов и молекул, энергия их колебательного движения, потенциальная энергия взаимодействия атомов и молекул, кинетическая и потенциальная энергия электронов в атомах, внутриядерная энергия. Однако в большинстве физических явлений, в которых участвуют термодинамические системы, не все перечисленные виды энергии испытывают изменения. В частности, внутриатомная энергия в таких процессах не участвует. Поэтому, употребляя понятие внутренней энергии, имеют в виду не полную энергию данной системы, а только ту её часть, которая изменяется в рассматриваемых явлениях.

Внутренняя энергия системы является однозначной функцией её состояния. Это означает, в каждом определённом состоянии система обладает вполне определённым значением внутренней энергии; всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от процесса, приведшего систему из одного состояния в другое. Следовательно, при переходе системы из одного состояния в другое изменение её внутренней энергии будет всегда равно разности значений внутренней энергии U₁ и U₂ в этих состояниях . Однако следует заметить, при данной внутренней энергии система может находиться в различных состояниях.

Внутренняя энергия термодинамической системы может быть рассчитана в зависимости от значений всех физических величин, определяющих это состояние: V, Р, Т и т. д. Для тел, находящихся в твёрдом или жидком состоянии расчёт внутренней энергии затруднён и требует использования упрощающих предположений. Однако имеется довольно простой путь расчёта внутренней энергии для разряжённого газа в зависимости от его температуры. В параграфе 5.1. рассмотрена модель идеального газа; его частицы в среднем находятся далеко друг от друга и слабо взаимодействуют между собой. При этих условиях потенциальной энергией взаимодействия частиц можно пренебречь и тогда внутренняя энергия идеального газа определяется только кинетической энергией теплового движения его частиц. В последнем абзаце параграфа 5.2. показано, кинетическая энергия теплового движения частицы , и аналитическая запись внутренней энергия идеального газа принимает вид: U = = N × .

В самом общем случае рассматриваемая термодинамическая система, обмениваясь энергией со средой или окружающими телами, может получать или отдавать количество теплоты Q, может производить работу или над ней может быть произведена работа А. Следовательно, тепло и работа – две формы, в которых энергия системы может передаваться среде или, наоборот, энергия среды может передаваться термодинамической системе. По закону сохранения энергии исключается возможность каких-либо потерь при энергетическом обмене. Естественно, разность энергий термодинамической системы в двух состояниях должна равняться сумме теплоты и работы, полученных системой из окружающей среды: ; здесь – работа, совершаемая внешними телами над системой; Q – количество сообщённого системе тепла; U₁ и U₂ – начальное и конечное значения внутренней энергии термодинамической системы. Поскольку внутренняя энергия системы является функцией состояния, прирост энергии при переходе термодинамической системы из одного состояния в другое всегда один и тот же и не зависит от характера или способа перехода от начального состояния к конечному. Если измерять сообщённые системе теплоту и работу в различных переходах от одного и того же начального к одному и тому же конечному состоянию, прирост энергии во всех случаях должен быть одним и тем же. Выраженный в приведённой форме закон сохранения энергии носит название первого начала термодинамики. Аналитическая запись первого начала термодинамики для элементарного процесса имеет вид:

(1)

здесь d А – работа, совершаемая системой над внешними телами, при этом . Из аналитической записи первого начала термодинамики следует, количество тепла Q можно измерять в тех же величинах, что и работу или энергию. Единицей количества теплоты в СИ служит джоуль (Дж).

Работа в термодинамике

Ранее, в параграфе 6.1., мы говорили о равновесных состояниях термодинамической системы; в этих состояниях параметры системы одинаковы во всём её объёме. Приступая к рассмотрению работы в термодинамических системах, следует ожидать, что её совершение связано с изменением объёма системы. И тогда возникает вопрос, о каких же процессах идёт речь, если рассмотрению подлежат равновесные состояния? Ответ состоит в следующем: если процесс идёт медленно, то значения параметров состояния во всём объёме можно считать одинаковыми. Понятие «медленно» здесь следует уточнить. Прежде всего, оно связано с понятием «время релаксации» – временем, в течение которого устанавливается равновесие в системе. Нас сейчас интересует время выравнивания давления в системе (время релаксации), когда термодинамической системой совершается работа, связанная с изменением объёма; для однородного газа это время составляет ~ 10^–16 с. Очевидно, время релаксации достаточно незначительно по сравнению со временем протекания процессов в реальных термодинамических системах (или по сравнению со временем измерения). Естественно, мы вправе считать, что реальный процесс есть последовательность равновесных состояний и поэтому имеем право, изобразить его линией на графике V, P (рис. 6.1.). Разумеется, по осям координатной системы могут откладываться объём и температура или давление и температура. Поскольку в алгебре, и не только, при построении графиков первой координатной осью читается и записывается х, а затем – у, т. е.«х, у», есть надежда, что читатель, прочитывая «оси координатной системы V, Р», предполагает – по оси х откладывается объём V, а по оси у – давление газа Р.

Ознакомимся с видом линий, отображающих графически простейшие процессы в системе координат, по осям которой отложены параметры состояния V, P (возможны иные координатные оси). Выбор координатной системы обусловлен тем, что площадь, ограниченная кривой процесса и двумя крайними координатами для начального и конечного значений объёма, равна работе сжатия или расширения. На рис. 6.2. приведены графики изопроцессов, проведённые из одного и того же начального состояния. Кривая адиабатического процесса (адиабата) идёт круче, чем для изотермического процесса (изотерма). Это обстоятельство можно объяснить на основании уравнения Клапейрона для состояния газов:

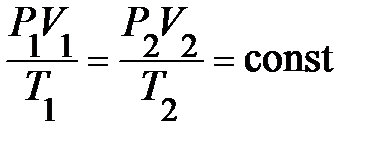. (2)

Выражая из уравнения состояния Р ₁ и Р ₂, разность давлений при расширении газа от объёма V ₁ до объёма V ₂ запишется:

. (3)

Здесь, как и в уравнении (2), .

При адиабатическом расширении работа над внешними телами совершается только за счёт внутренней энергии газа, вследствие чего внутренняя энергия, а вместе с ней и температура газа уменьшаются; т. е. в конце адиабатического процесса расширения (см. рис. 6.2.) Т ₂ Т ₁ (найдите обоснование); при изотермическом же процессе Т ₂ = Т ₁. Поэтому в формуле (3) разность давлений будет больше при адиабатическом расширении, чем при изотермическом расширении (проверьте, проведя преобразования).

Осознав, что мы имеем дело с равновесными процессами и ознакомившись с их графическим отображением в системе координат (V, P), перейдём к поиску аналитического выражения внешней работы, совершаемой термодинамической системой.

Работа, совершаемая системой, может быть вычислена в зависимости от значения внешних сил, действующих на систему, и от величины деформации системы – изменения её формы и размеров. Если внешние силы приложены по поверхности в виде, например, внешнего давления, сжимающего систему, то расчёт внешней работы может быть произведён в зависимости от изменения объёма системы. Для иллюстрации рассмотрим процесс расширения газа, заключённого в цилиндре с поршнем (рис. 6.3.). Допустим, что внешнее давление на всех участках по поверхности цилиндра одно и то же. Если при расширении системы поршень сместился на расстояние , то элементарная работа, совершённая системой, запишется здесь S – площадь поршня, а – изменение объёма системы (рис. 6.3.). При расширении системы внешнее давление не всегда остаётся постоянным, поэтому работа, совершаемая системой при изменении её объёма от V ₁ до V ₂, должна рассчитываться как сумма элементарных работ, т. е. путём интегрирования: . Из уравнения работы следует, параметры начального (p ₁, V ₁) и конечного (p ₂, V ₂) состояний системы не определяют величину совершаемой внешней работы; необходимо знать ещё и функцию р (V), раскрывающую изменение давления в процессе перехода системы из одного состояния в другое.

В заключение этого параграфа следует заметить, теплообмен между системой и окружающей средой зависит не только от параметров начального и конечного состояний системы, но и от той последовательности промежуточных состояний, через которые проходит система. Это следует из первого закона термодинамики: Q = U ₂ – U ₁ + A, где U ₁ и U ₂ определяются только заданием параметров начального и конечного состояний, а внешняя работа A зависит, кроме того, ещё и от самого процесса перехода. Вследствие этого теплота Q, полученная или отданная системой при переходе из одного в другое состояние, не может быть выражена в зависимости только от температуры её начального и конечного состояний.

Завершая экскурс в раздел «Термодинамика. Первое начало термодинамики», перечислим его ключевые понятия: термодинамическая система, термодинамические параметры, равновесное состояние, равновесный процесс, обратимый процесс, внутренняя энергия системы, первое начало термодинамики, работа термодинамической системы, адиабатический процесс.