В отличие от твёрдых тел в жидкости возможны значительные смещения составляющих её частиц относительно друг друга. Поэтому для жидкости, как и для твёрдых тел, характерно наличие вполне определённого объёма, чего нельзя сказать о газе. Вместе с тем жидкость, подобно газу, принимает форму сосуда, в который её помещают. Как показывают рентгенографические исследования, в отношении характера расположения частиц жидкости также занимают промежуточное положение между твёрдыми телами и газами. В расположении частиц жидкости наблюдается ближний порядок. Это означает, по отношению к любой частице расположение ближайших к ней соседей является упорядоченным. Однако по мере удаления от данной частицы расположение по отношению к ней других частиц становится всё менее упорядоченным и чем дальше от частицы – порядок в расположении частиц полностью исчезает. В кристаллах имеет место дальний порядок – упорядоченное расположение частиц по отношению к любой частице наблюдается в пределах значительного объёма. Наличие в жидкости ближнего порядка послужило причиной того, что структуру жидкостей называют квазикристаллической – кристаллоподобной.
| Рис.4.1. 4.1. |
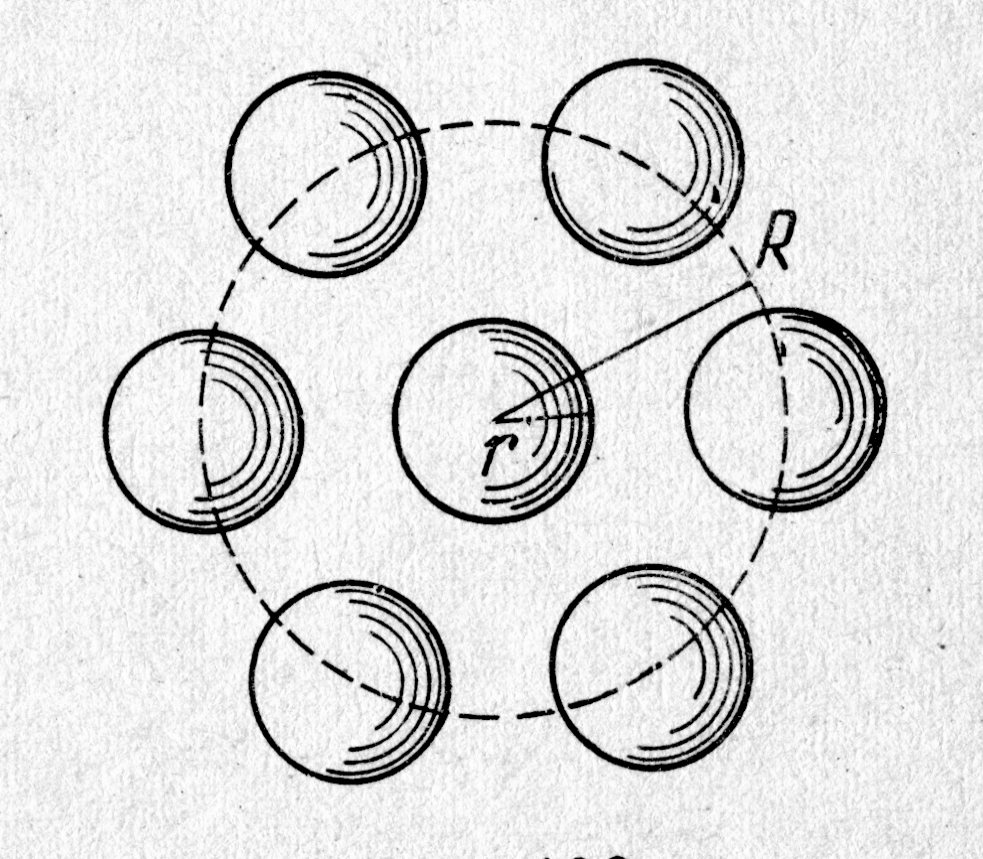
 R в среднем равна нулю (рис. 4.2., см. а, б). Иначе обстоит дело, если молекула находится на расстоянии от поверхности меньшем, чем R. Так как плотность газа (пара), с которым граничит жидкость, во много раз меньше плотности жидкости, выступающая за пределы жидкости часть сферы молекулярного действия будет менее заполнена молекулами. Естественно, результирующая сила, действующая на молекулу, не равна нулю и направлена внутрь жидкости перпендикулярно её поверхности (рис. 4.2., см. в, г). Величина этой силы растёт в направлении от внутренней к наружной границе слоя жидкости. В таком положении находятся все молекулы, лежащие в поверхностном слое жидкости толщиной, ~ равной радиусу сферы молекулярного действия R = 1,5×10–7 см. Таким образом, поверхностный мономолекулярный слой жидкости оказывает на всю жидкость давление; его принято называть внутренним или молекулярным. Аналитически его можно записать p = DF/DS, где DF – сила молекулярного взаимодействия на площади сплошной среды DS.
R в среднем равна нулю (рис. 4.2., см. а, б). Иначе обстоит дело, если молекула находится на расстоянии от поверхности меньшем, чем R. Так как плотность газа (пара), с которым граничит жидкость, во много раз меньше плотности жидкости, выступающая за пределы жидкости часть сферы молекулярного действия будет менее заполнена молекулами. Естественно, результирующая сила, действующая на молекулу, не равна нулю и направлена внутрь жидкости перпендикулярно её поверхности (рис. 4.2., см. в, г). Величина этой силы растёт в направлении от внутренней к наружной границе слоя жидкости. В таком положении находятся все молекулы, лежащие в поверхностном слое жидкости толщиной, ~ равной радиусу сферы молекулярного действия R = 1,5×10–7 см. Таким образом, поверхностный мономолекулярный слой жидкости оказывает на всю жидкость давление; его принято называть внутренним или молекулярным. Аналитически его можно записать p = DF/DS, где DF – сила молекулярного взаимодействия на площади сплошной среды DS.
| Рис.4.2. 4.2. |
Характерной особенностью жидкостей и газов является то, что они не оказывают сопротивления сдвигу и поэтому легко изменяют свою форму. Однако для изменения объёма жидкости или газа требуются конечные внешние силы. При изменениях объёма, происходящих в результате внешних воздействий, в жидкостях или газах возникают упругие силы, уравновешивающие действие внешних сил. Упругие свойства жидкостей и газов проявляются в том, что отдельные части их действуют друг на друга (и на соприкасающиеся с ними тела) с силой, зависящей от степени сжатия жидкости или газа. Это воздействие характеризуется величиной, называемой давлением. Учитывая результаты параграфа 3.4., можно сказать, сила давления действует на каждый макроскопический элемент (D N << N) жидкости или газа и на жидкость или газ в целом, но не имеет смысла для отдельной частицы среды.

| Рис. 4.3. |
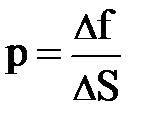 . Давление является скалярной величиной, поскольку его значение не зависит от ориентации площадки DS. Математика не противоречит такому утверждению. Действительно, давление, по существу, равно отношению двух коллинеарных векторов
. Давление является скалярной величиной, поскольку его значение не зависит от ориентации площадки DS. Математика не противоречит такому утверждению. Действительно, давление, по существу, равно отношению двух коллинеарных векторов 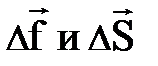 , а такая величина представляет собой скаляр (проверьте); здесь имеется в виду, площадка DS может рассматриваться как вектор, имеющий направление нормали к DS.
, а такая величина представляет собой скаляр (проверьте); здесь имеется в виду, площадка DS может рассматриваться как вектор, имеющий направление нормали к DS.Давление в газе определяется аналогичным образом.
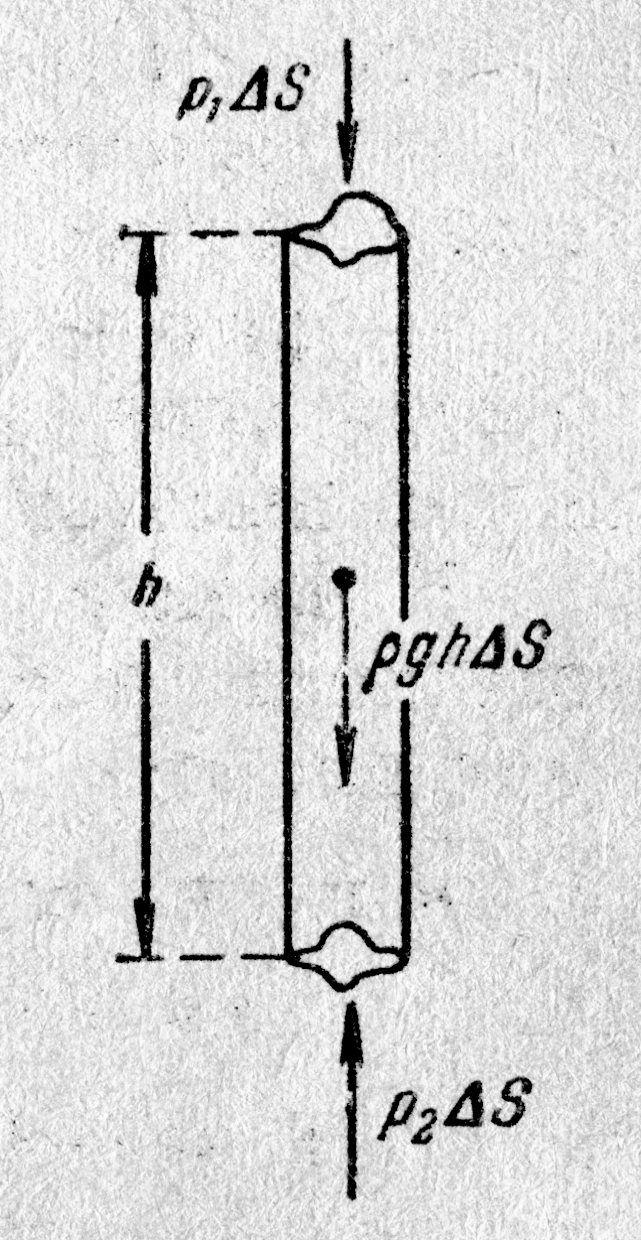
Если бы в жидкости (или газе) не было объёмных сил, то условием равновесия было бы постоянство давления во всём объёме. Рассмотрим распределение давления в жидкости при наличии объёмных сил. Для этого выделим цилиндрический объём жидкости таким образом, чтобы его ось была вертикальной (рис. 4.4.). В этом случае вдоль оси цилиндра, кроме сил давления на основания, будет действовать также объёмная сила тяжести m × g = r × g × h × DS (r – плотность жидкости, h – высота цилиндра, столба жидкости) и условие равновесия имеет вид:
 .
.
Сокращая на DS, имеем
 ,
,
давления на двух разных уровнях отличаются на величину, численно равную весу вертикального столба жидкости, заключённого между этими уровнями. По этой формуле рассчитывается давление внутри покоящейся жидкости на глубине h от открытой горизонтальной поверхности.
| Рис. 4.4. |
 .
.
После преобразований читатель может получить хорошо известное выражение для силы Архимеда: 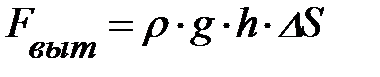 , которое может быть прочитано так – равнодействующая всех сил давления, приложенных к поверхности тел, погружённых в жидкость или газ, направлена вертикально вверх и равна весу жидкости или газа в объёме данного тела. Если средняя плотность тела меньше, чем плотность жидкости, то в состоянии равновесия тело будет погружено в жидкость только частично. При этом сила тяжести, приложенная к центру тяжести тела, и выталкивающая сила, приложенная к центру тяжести погруженной в жидкость части объёма тела, должны быть равны по величине, и действовать вдоль одной и той же прямой; иначе создадут вращающий момент.
, которое может быть прочитано так – равнодействующая всех сил давления, приложенных к поверхности тел, погружённых в жидкость или газ, направлена вертикально вверх и равна весу жидкости или газа в объёме данного тела. Если средняя плотность тела меньше, чем плотность жидкости, то в состоянии равновесия тело будет погружено в жидкость только частично. При этом сила тяжести, приложенная к центру тяжести тела, и выталкивающая сила, приложенная к центру тяжести погруженной в жидкость части объёма тела, должны быть равны по величине, и действовать вдоль одной и той же прямой; иначе создадут вращающий момент.




