В предыдущих параграфах (3.4., 4.1.) при описании вещества в модели сплошной среды нами рассматривались две простейшие ситуации. Либо мы имели дело с движением специфической «квазичастицы» индивидуального типа – малого элемента объёма среды D V, состоящего из одних и тех же атомов, вблизи фиксированного положения равновесия. При этом нам удалось получить достаточно подробное описание малых отклонений параметров среды от их равновесных значений с течением времени; например, уравнение волны.
Либо мы рассматривали сохраняющиеся физические величины, присущие сплошной среде, для одного и того же фиксированного конечного элемента объёма D V независимо от того, какие атомы находились в нём в заданный момент времени. При таком подходе удалось получить некоторые представления о свойствах сплошной среды в целом, атомы которой способны совершать произвольное поступательное движение. В частности, это относится к плотности и давлению сплошной среды.
Из всего сказанного следует, важнейшая особенность макроскопических элементов сплошной среды как «частиц» состоит в том, что они не могут двигаться независимо. Любое их движение должны быть таким, чтобы не разрушить целостность среды. Для выяснения условия, обеспечивающего «непрерывность» сплошной среды, полезно обратиться к закону сохранения массы, справедливому в нерелятивистском приближении; скорость движения элементов среды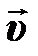 
много меньше скорости света 
, 
.
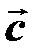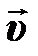
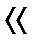
| Рис. 4.5. |
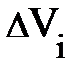
| DVi |
| DVi |
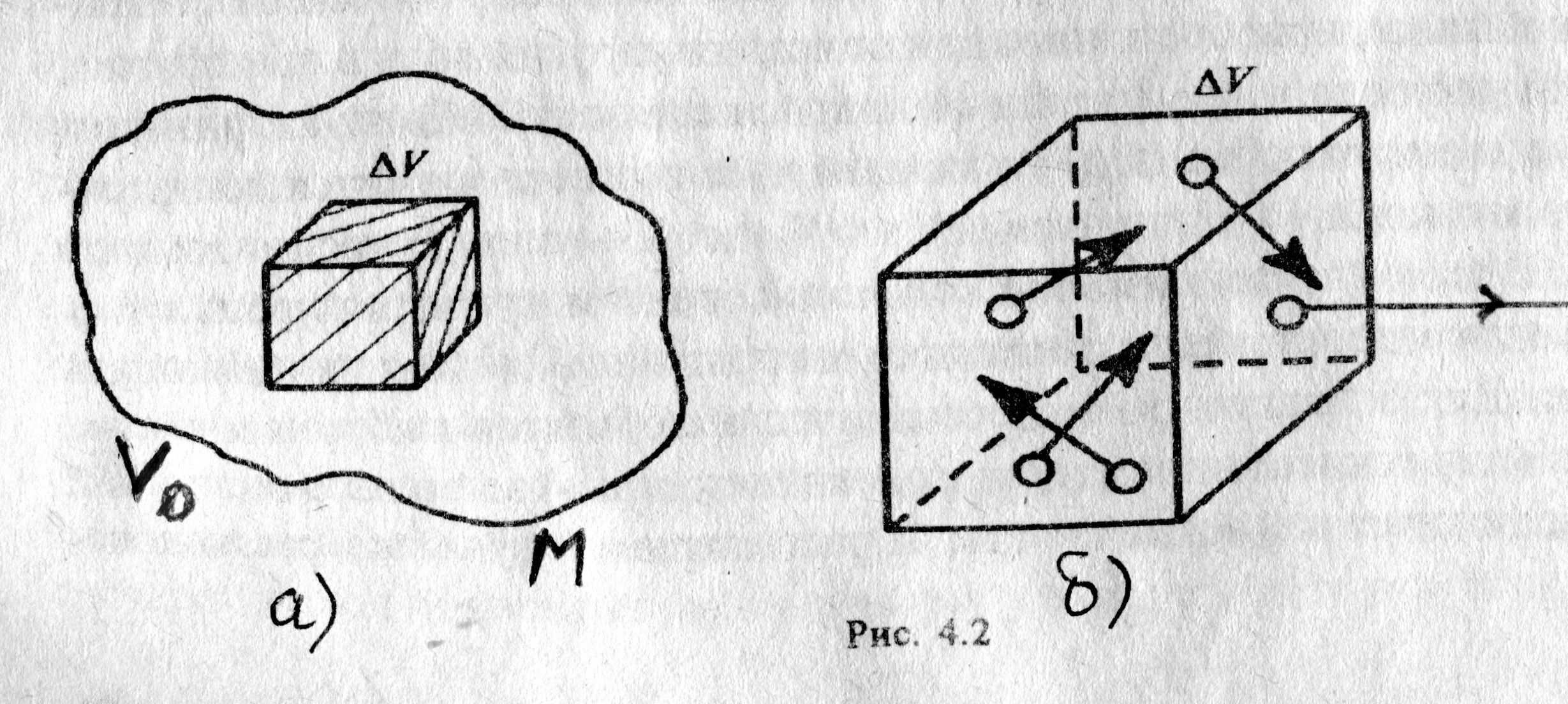
Пусть у нас есть изолированный макроскопический объект сплошной среды (жидкости или газа) объёмом
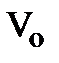(рис. 4.5. а), полная масса которого М постоянная (равна const). Разобьём его мысленно на элементы объёма 
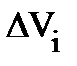, имея в виду, что 
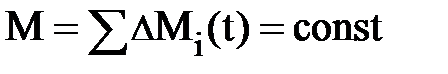(рис. 4.5. а); здесь 
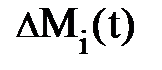– переменная масса, заключённая в объёме 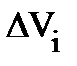, причём 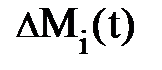= r(r,t)× 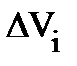. Будем считать, что плотность вещества в элементе 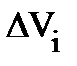равна плотности макроскопического объекта сплошной среды, 
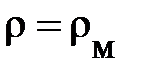.Поскольку масса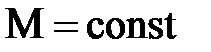 
, т.е. остаётся постоянной, массы 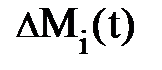разных элементов объёма 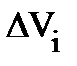должны меняться со временем согласованно. Изменение массы в каждом элементе объёма 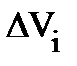проявляется в том, что плотность среды r(r,t) зависит от времени. Однако ввиду сохранения массы во всём теле, в целом эти изменения могут возникнуть только потому, что какое-то число молекул в каждый момент времени покидает элемент объёма 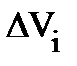, а какое-то другое их число попадает вновь в этот элемент. Другими словами, имеется поток массы переносимый молекулами через поверхность, ограничивающую объём 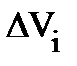(рис. 4.5. б). Стрелками показано движение молекул через поверхность элемента объёма 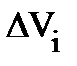. Таким образом, поскольку источники массы внутри объёма отсутствуют, то изменение массы в объёме 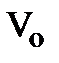в единицу времени равно потоку массы переносимому частицами через поверхность 
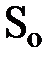этого объёма. Аналитически это может быть записано 
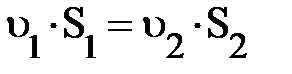. Эту формулу называют уравнением неразрывности потока.
Если плотность среды со временем не изменяется, сплошная среда называется стационарной. В стационарном случае вводят понятие трубки тока. Ею называется всякий объём сплошной среды (жидкой или газообразной), боковые стенки которого (рис. 4.6.) образованы линиями тока. Трубка тока выделена тем, что вдоль её боковой поверхности всюду скорость перпендикулярна площади потока S. При этом поток через боковую поверхность отсутствует (рис. 4.6.). В этом случае смысл закона неразрывности потока прост – вдоль трубки тока расход стационарной среды не изменяется и модуль скорости всегда обратно пропорционален сечению трубки тока.
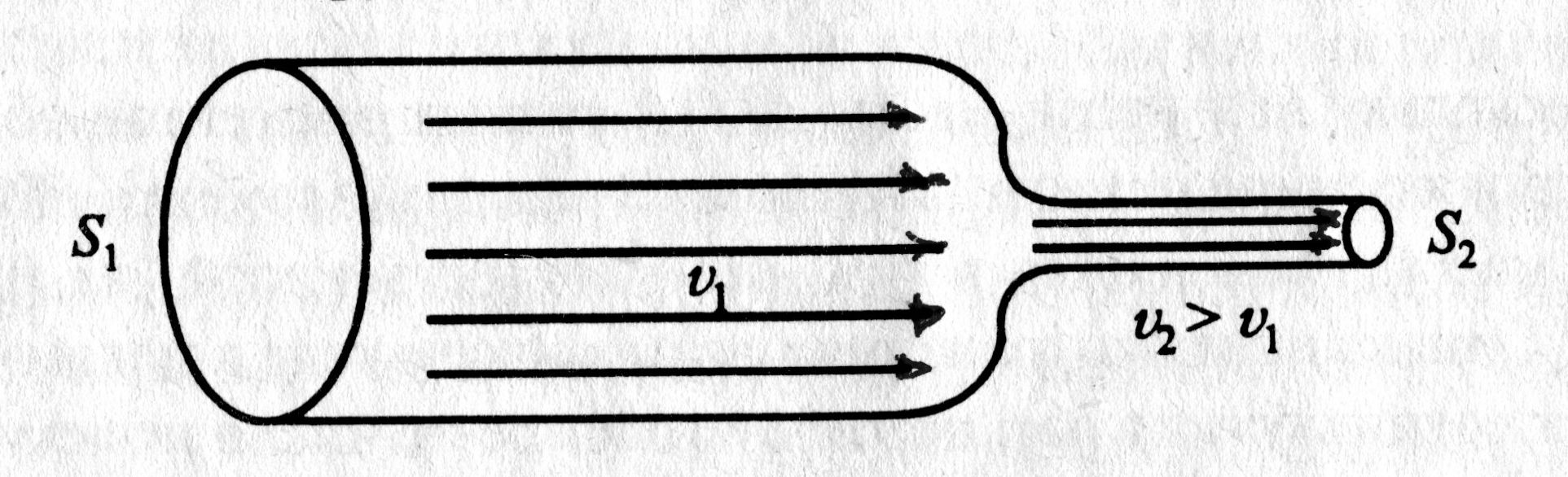
| Рис. 4.6. |
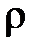= const; (разумеется, для газов такое предположение несправедливо). При таком приближении речь может идти только о рассмотрении поступательного движения элемента жидкости во внешних потенциальных полях сил. К их числу относятся как объёмные силы, в частности, гравитационные, действующие на каждую частицу жидкости, так и упругие силы, вызываемые давлением на элемент жидкости в целом со стороны стенок сосуда. В этом предельном случае роль сохраняющейся величины играет механическая энергия элемента жидкости.Выделим в стационарно текущей идеальной жидкости трубку тока (рис. 4.7.). Рассмотрим объём жидкости, ограниченный стенками трубки тока (реальной трубы). Будем считать, линии тока перпендикулярны сечениям трубки тока S1 и S2. За малое время Dt сквозь сечение S1 пройдёт эле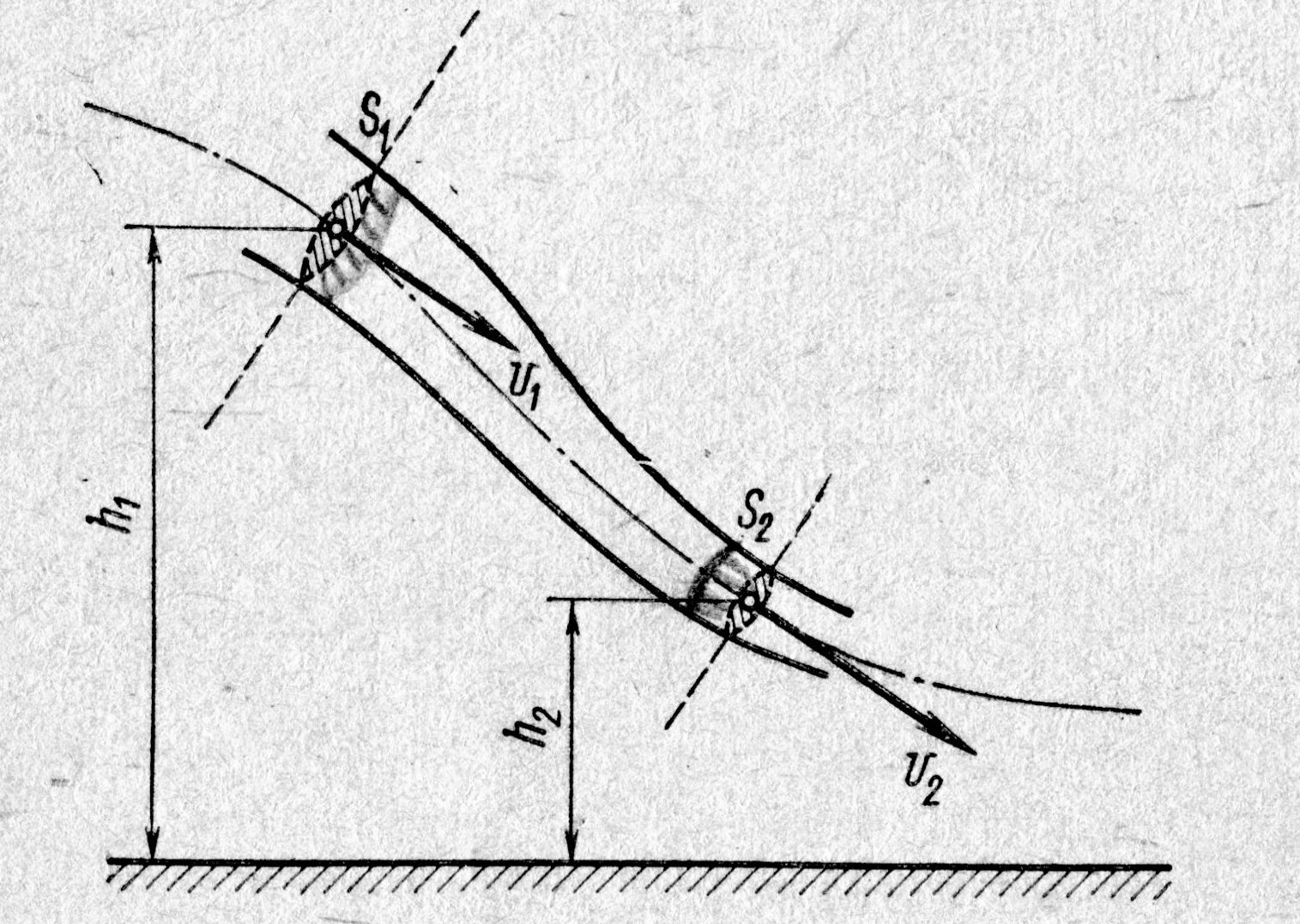 
| Рис. 4.7. |
| P1 |
| P2 |
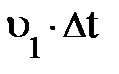; каждый объём прошедшей через S1 жидкости массой m = r×DV1 несёт кинетическую энергию 
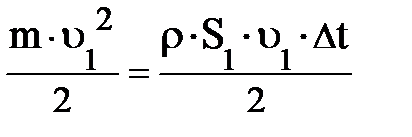и потенциальную энергию m×g×h1 (рис. 4.7.). Внешняя сила 
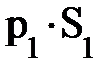, действующая в сечении S1, смещает указанный объём жидкости DV1 на расстояние 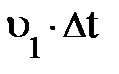и поэтому совершает положительную работу, равную 
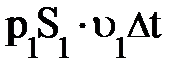(рис. 4.7.).
В приближении идеальной и несжимаемой жидкости, и приняв во внимание уравнение неразрывности потока, нетрудно понять, через сечение S2 за то же самое время должен выйти тот же объём жидкости DV1; т.е. DV1 = DV2 = S2×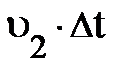 
. Здесь внешняя сила 
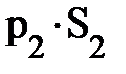совершает отрицательную работу, равную 
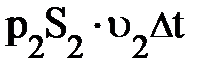. Иных изменений в данной области не происходит. Поэтому изменение полной энергии DW равно разности полных энергий втекающей и вытекающей масс. Учитывая, что полная энергия слагается из кинетической и потенциальной составляющих, получим
DW = (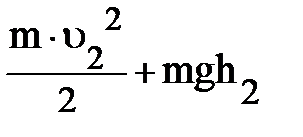
) – (
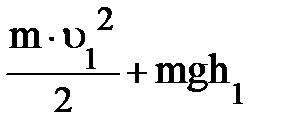) (1)
В соответствии с законом сохранения энергии изменение энергии, представленное уравнением (1), равно работе DА внешних сил (давления) по перемещению массы жидкости m 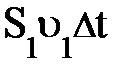= r 
= r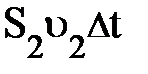 
; т.е. DW = DА. Поэтому DА может быть записано
DА =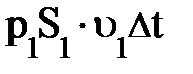 
– 
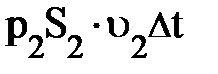(2)
Приравняв правые части уравнений (1) и (2), читатель может самостоятельно получить уравнение Бернулли. Действительно, если учесть уравнение неразрывности потока, m = r×DV1 = r×DV2, а отсюда следует 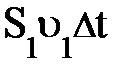= 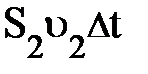, тогда 
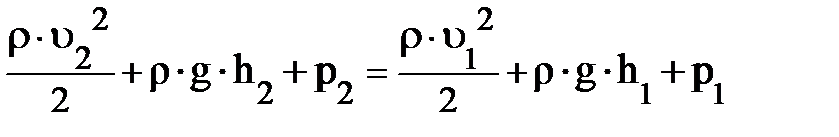(преобразования самостоятельно проделали?). Поскольку выбор сечений S1 и S2 произволен, уравнение Бернулли записывается в виде:
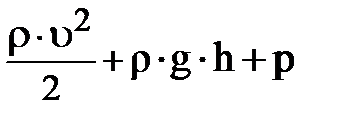= const (3)
Следовательно, в установившемся потоке идеальной жидкости полное давление, слагающееся из динамического, гидравлического и статического давлений, постоянно на любом поперечном сечении потока. Уравнение (3) применимо и для газа. Это допустимо, если, например, воздух движется со скоростью не превышающей ~ 200 м/с; вязкостью и сжимаемостью газа при таком движении ещё можно пренебречь.
4.3. Давление под искривлённой поверхностью жидкости.
Капиллярные явления
В параграфе 4.1., рис. 4.2. мы выяснили (посмотрели?), в приповерхностном слое жидкости на молекулу действует равнодействующая сил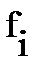 
, направленная в внутрь жидкости 
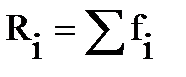; отобразим её на рис. 4.8., слева.
| Рис. 4.8. |
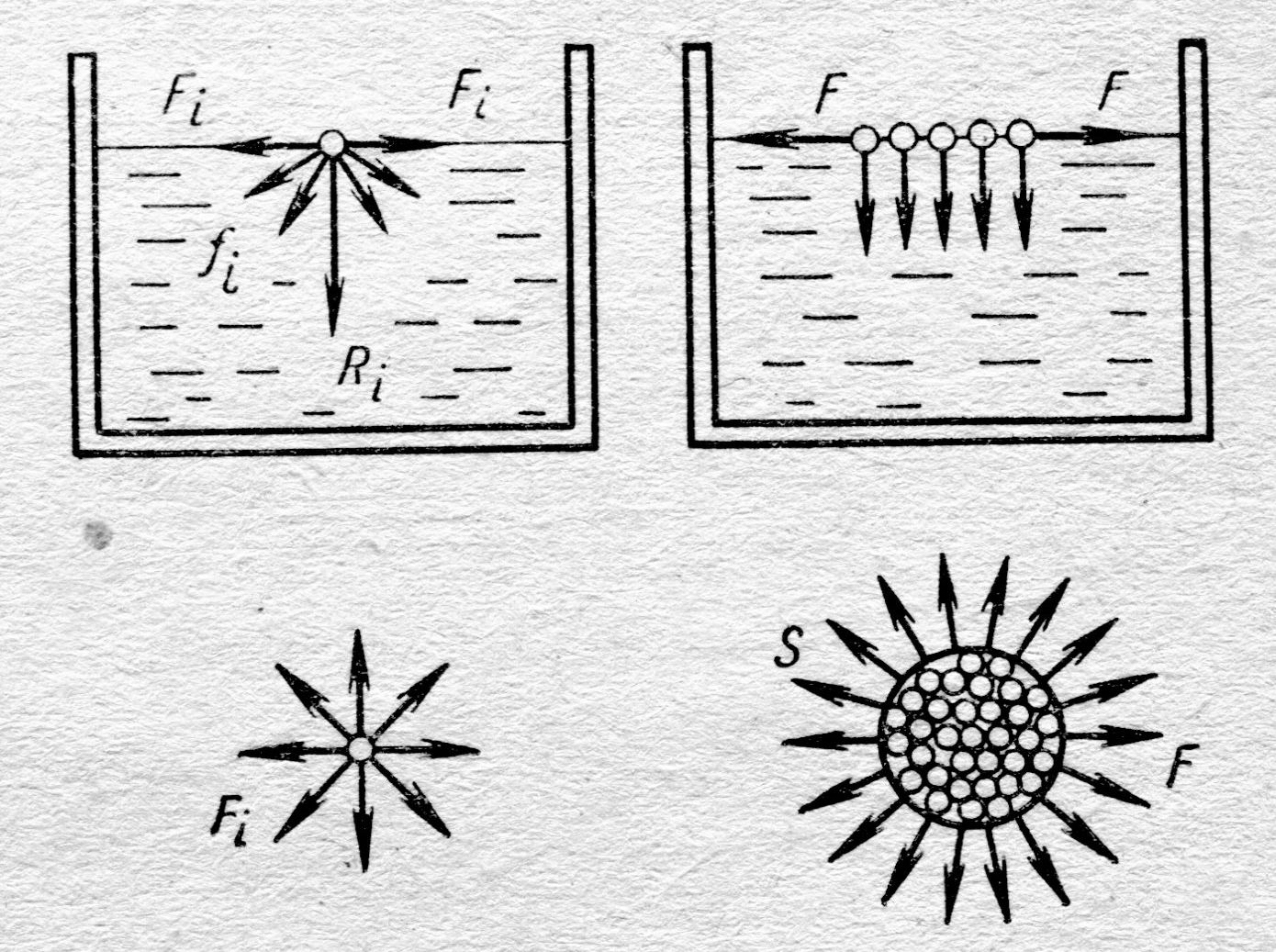Кроме того, на молекулы поверхностного слоя действуют силы 
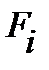, лежащие в плоскости, касательной к поверхности жидкости (см. рис. 4.8., справа). Эти внешние силы F, растягивающие плёнку, и называют силами поверхностного натяжения. Если выделить на поверхности жидкости площадку S, рис. 4.8., справа (внизу), то силы F, направленные наружу, являются внешними силами; они перпендикулярны периметру площадки S и касательные к поверхности жидкости. Для всех молекул, лежащих внутри площадки S, все эти силы 
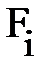взаимно уравновешиваются.
Всё сказанное об особых условиях, в которых находятся молекулы поверхностного слоя жидкости, в целом относится и к твёрдым телам. Следовательно, твёрдые тела, как и жидкости, обладают поверхностным натяжением. Следует ожидать, если жидкость имеет границу с твёрдым телом, то эта система, с учётом сил межмолекулярного взаимодействия, принимает конфигурацию, соответствующую минимуму суммарной потенциальной энергии; поверхностной, с учётом и поля сил тяжести. В частности, это проявляется на искривлении поверхности жидкости; явление смачивания (не смачивания, например, ртуть).
Под искривлённой поверхностью жидкости помимо внутреннего давления силы поверхностного натяжения создают дополнительное давление на жидкость. Оно прибавляется к давлению, созданному поверхностным слоем, или вычитается из него. Кстати, давление, создаваемое поверхностным слоем воды ~ 1,7×109 Па, что значительно превышает давление атмосферы; поэтому все жидкости уже сильно сжаты внутренними молекулярными силами. Чтобы вызвать дополнительное уменьшение их объёма, сжать, требуется приложить очень большое внешнее давление. (Вспомните неудачные прыжки в воду в детские годы; «нежная» при умывании вода, больно жалит при взаимодействии с нею за малый промежуток времени.)
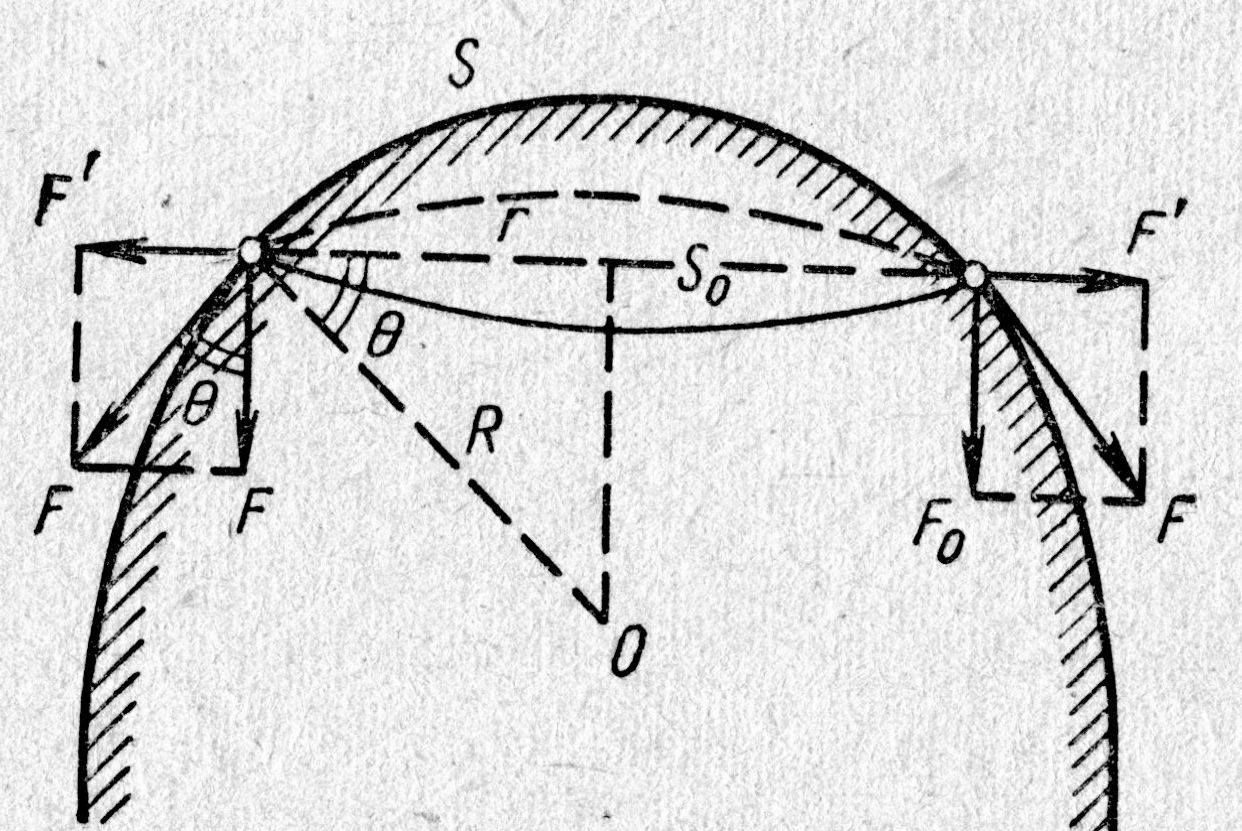
| Рис. 4.9. |
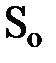; радиус основания 
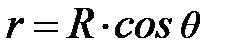(см. рис. 4.9.). Силы поверхностного натяжения 
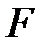, действующие по периметру площадки S (рис. 4.9.), создают равнодействующую 
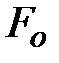, перпендикулярную основанию 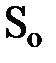и равную 
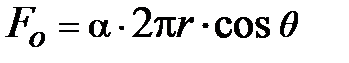. Составляющие 
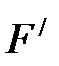силы поверхностного натяжения 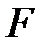в сумме дают нуль (почему? Нарисуйте вид сверху, поможет). Учитывая, что давление равно силе приходящейся на единицу площади, т.е., 
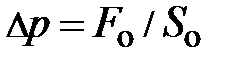, для дополнительного давления на жидкость от сил поверхностного натяжения, обусловленного кривизной поверхности, получим аналитическое выражение 
.
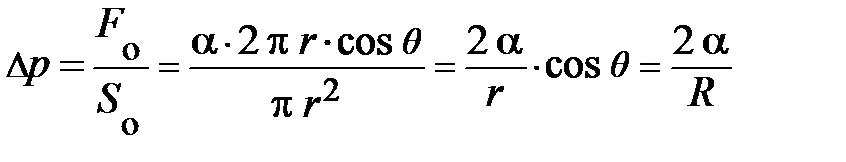| Рис. 4.10. |
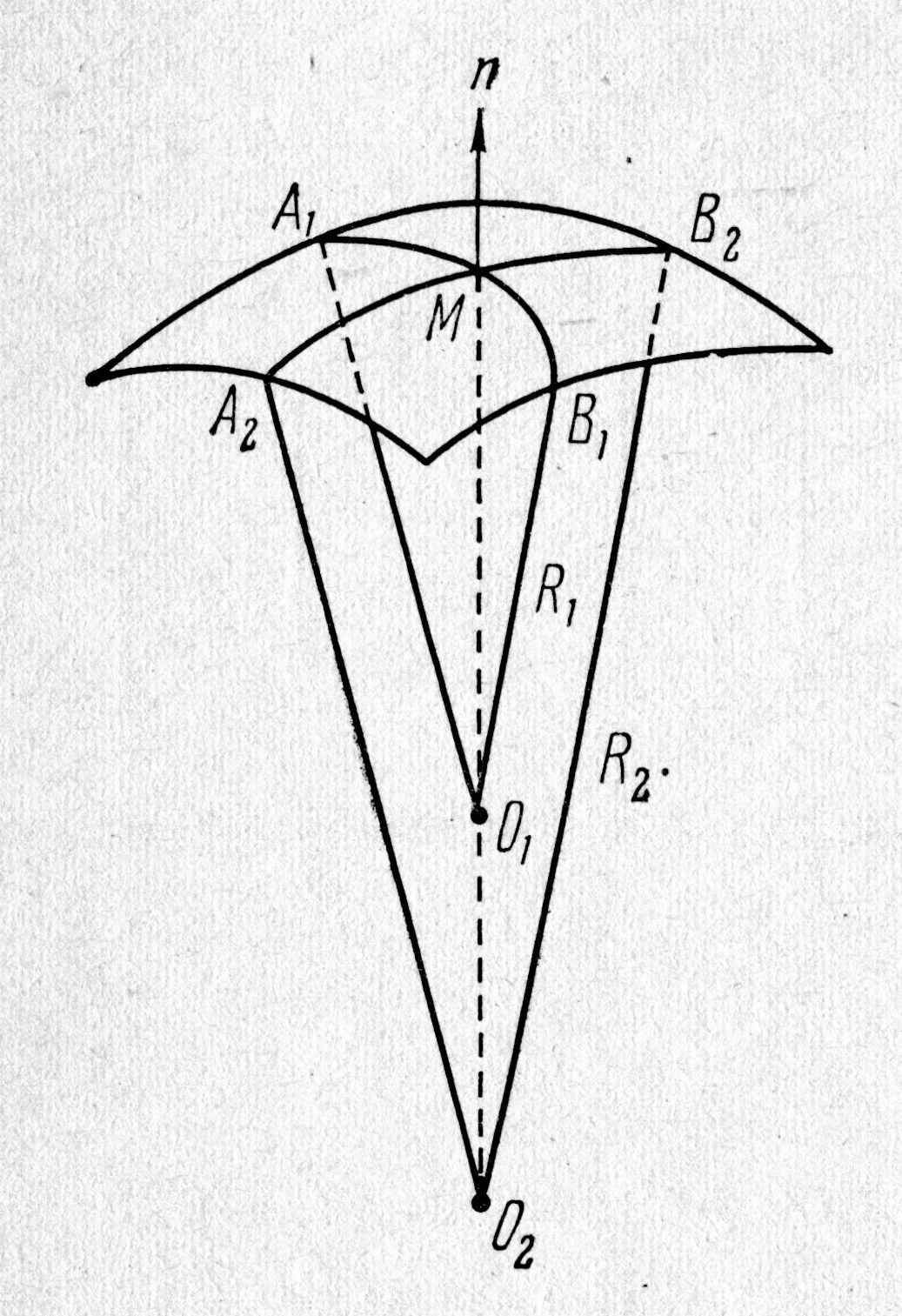
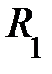и максимальный 
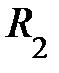; они лежат во взаимно перпендикулярных плоскостях и называются главными радиусами кривизны поверхности S в данной её точке (рис. 4.10.). Точное выражение для дополнительного давления под искривлённой поверхностью жидкости любой формы вывел французский математик и физик Лаплас в 1805 году. Оно может быть представлено в виде 
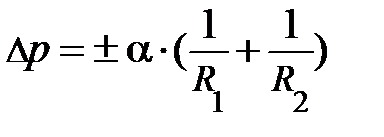. Знак плюс соответствует выпуклой поверхности, знак минус – вогнутой поверхност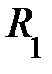и; 
и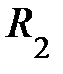 
здесь алгебраические величины – если центр кривизны находится под данной поверхностью, радиус кривизны положительный; если центр кривизны лежит над поверхностью, радиус кривизны отрицателен (отобразите на рис; сделали?).
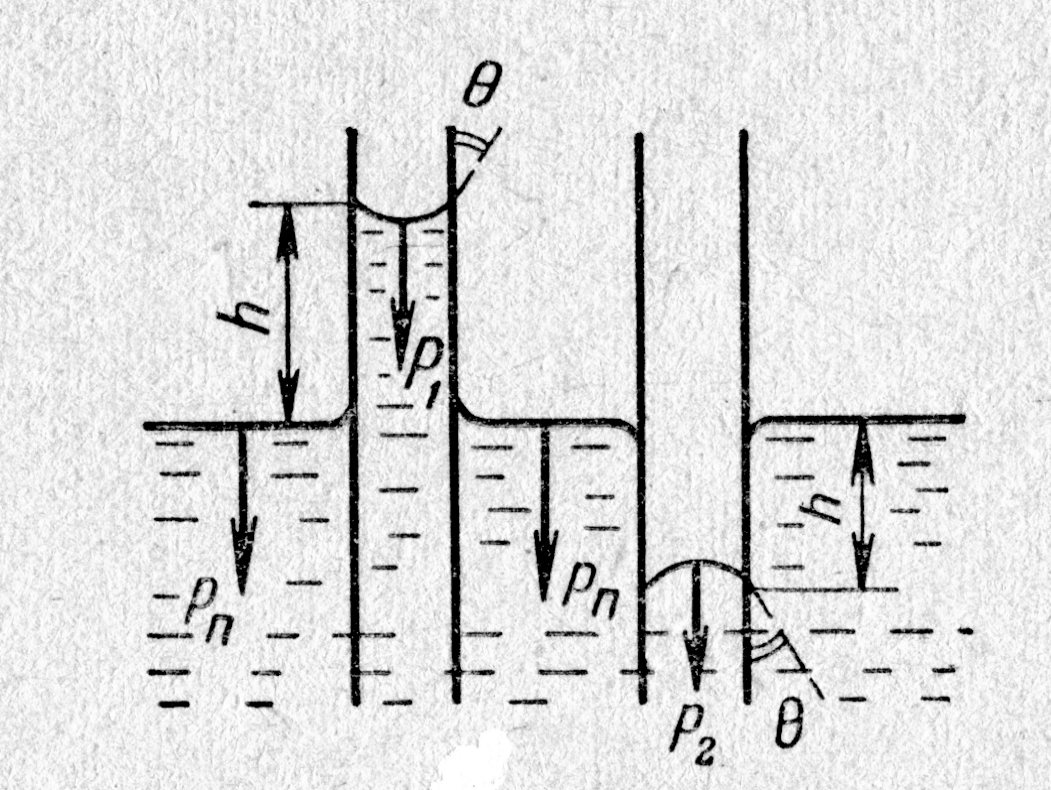
| Рис. 4.11. |
Если силы сцепления между молекулами жидкости больше, чем между молекулами жидкости и твёрдого тела, то жидкость, искривляясь, стремится уменьшить границу соприкосновения с твёрдым телом, т.е. сжимается, «опускается» по стенкам (рис. 4.11., справа); в этом и состоит суть явления несмачивания. Изогнутую поверхность принято называть мениском, а узкую трубку (щель и т.п.) – капилляром.
При большой кривизне мениска внутреннее давление жидкости в капилляре (на уровне горизонта поверхности) будет меньше, чем вне капилляра, на величину избыточного давления под искривлённой (сферической) поверхностью. По закону Паскаля это должно сопровождаться выдавливанием вверх жидкости в капилляре (при смачивании, рис. 4.11., слева). Жидкость в капилляре поднимается до тех пор, пока давление столба жидкости не скомпенсирует уменьшение давления, обусловленное искривлением поверхности жидкости; давление столба жидкости должно равняться капиллярному давлению. Аналитически это запишется D р =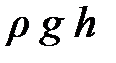 
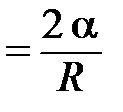. В случае же несмачивания давление в капилляре возрастает, что сопровождается понижением уровня жидкости в капилляре (рис. 4.11., справа). Попробуйте записать аналитически и описать словами, сопровождая свои действия рисунками. Капиллярные явления широко распространены в природе и технике. Где и как?
Завершая экскурс в раздел «Элементы механики сплошных сред: жидкости и газы», перечислим его ключевые понятия: квазикристаллическая структура, сфера молекулярного действия, молекулярное давление, макроскопический элемент, гидростатическое давление (объёмные силы), уравнение неразрывности потока, трубка тока, идеальная несжимаемая жидкость, искривлённая поверхность, капиллярное (лапласовское) давление.
