Квазиупругая сила
В предыдущем параграфе было установлено, несмотря на большое разнообразие колебательных процессов, как по физической природе, так и по степени сложности, все они совершаются по общим закономерностям и могут быть сведены к простейшим, гармоническим колебаниям, совершаемым по закону х (t) = 
. Настала пора уточнить физическое содержание уравнения. Для наглядности представим колебания математического и пружинного маятников на рис. 3.2.. Из рисунка следует, в уравнении колебания х (t) х – смещение колеблющегося тела из положения равновесия в заданный момент времени t, х о – максимально возможное отклонение из положения равновесия, амплитуда колебания. Графически уравнение колебания представлено на рис. 3.3. сплошной линией. Здесь jо = 0 – начальная фаза, определяющая положение тела, совершающего колебательный процесс, в момент времени t = 0. 
– фаза колебания, однозначно определяющая положение тела в заданный момент времени, а 
– текущая фаза колебания; 
– циклическая частота, определяющая число колебаний за 2p секунд, а T – период колебаний, время одного полного колебания. Наряду с периодом в технике используется величина обратная периоду и называемая частотой колебаний; её обозначают греческой буквой ню, n = 1/Т – сколько раз в единицу времени повторяется одно и то же состояние колеблющегося тела; 
– тригонометрическая функция, определяющая закон движения тела.
Следует ожидать, скорость тела, как и смещение, должна изменяться по гармоническому закону. Взяв производную от смещения х по времени, находим 
; здесь учтено, начальная фаза jо = 0. Произведение амплитуды колебания х о на циклическую частоту w называют амплитудой скорости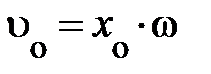 
или максимальным значением скорости. Тогда аналитическое выражение скорости принимает вид 
; график скорости представлен на рис. 3.3. крупным пунктиром и сдвинут по отношению к графику перемещения на p/2; из него следует, максимальное значение скорости соответствует минимальному значению перемещения и наоборот. Убедились в этом по графику?
Уравнение скорости функционально зависит от времени, следовательно, колебательное движение совершается с ускорением. Ускорение можно найти, продифференцировав уравнение скорости по времени:
Графически уравнение ускорения представлено на рис. 3.3. мелким пунктиром. Если учесть, 
, а 
формулу ускорения можно выразить через смещение х, то есть 
.
Сравнение формул смещения, скорости и ускорения приводит к следующим выводам: изменение этих физических величин совершается по закону синуса или косинуса с одинаковой циклической частотой или периодом 
; амплитуды этих колебаний различны и равны соответственно, 
– у смещения, 
– у скорости и 
– у ускорения. Фазы колебаний также различны – изменение скорости опережает изменение смещения по фазе на 
, что соответствует времени Т/4; изменение ускорения опережает изменение смещения в колебательном процессе на 
, что соответствует времени Т/2; здесь Т – период колебания. В этом можно убедиться, глядя на рис. 3.3..
В заключение следует обратить внимание на то, что по второму закону динамики сила, действующая на тело, совершающее колебательный процесс, запишется: F = ma = – m × 
. Отсюда может сложиться впечатление, что эта сила подобна упругой силе, поскольку она пропорциональна смещению х и имеет противоположный знак. Поэтому такого рода силы принято называть квазиупругими (как будто упругие). Почему? (см. с. 14, может оказать помощь).
