Законы сохранения в механике. Условия равновесия

Рис. 2.8.

Земля

Несмотря на то, что работа и энергия выражены в одинаковых единицах измерения, по сути это различные физические величины. В результате взаимодействия в замкнутой системе тел положение и скорость движущегося тела могут изменяться. Естественно, механическая энергия, будучи несозидаемой и неуничтожимой, в результате изменения механического состояния должна превращаться из одного вида в другой. Следовательно, энергия – количественная и качественная характеристика движения материи, а работа – количественная характеристика превращения одних форм движения в другие. Убедимся в этом на примере движения тела вблизи земной поверхности.

В качестве примера частного доказательства закона сохранения и превращения энергии рассмотрим падение тела с высоты Н (рис. 2.8.). Это, кстати, не единственный путь доказательства. Систему тело–Земля будем считать замкнутой (изолированной); тело не взаимодействует ни с какими иными телами или действие этих тел скомпенсировано. В начальном состоянии 1 кинетическая энергия тела К ₁ равна нулю, а потенциальная энергия может быть записана: П ₁ = m × g × H. Действительно, чтобы тело оказалось в состоянии 1 необходимо совершить работу против силы тяжести, поднять тело с поверхности Земли на высоту Н. Поскольку перемещение направлено вверх, а сила тяжести вниз совершённая работа по подъёму тела на высоту Н запишется: DА = mg×H. Учитывая, что работа равна изменению энергии взятой с противоположным знаком: DА = П ₁ – П _Зем. Принимая потенциальную энергию на поверхности Земли за нуль, получили ранее приведённое выражение.

В процессе перехода из состояния 1 в состояние 2 сила тяжести совершит работу DА = mg× (H – h) = – (П ₂ – П ₁). Поскольку работа является количественной характеристикой превращения одних форм движения в другие, а в предложенной ситуации потенциальной энергии в кинетическую, то: – (П ₂ – П ₁) = К ₂. Отсюда П ₁ = П ₂ + К ₂, и тогда это равенство можно прочитать так «полная механическая энергия замкнутой системы тел остаётся постоянной при переходе системы из одного состояния в другое». Здесь уместно заметить, механическая энергия, определяемая состоянием тела (х, 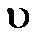), является одним из многих видов энергии (электрическая, электромагнитная, ядерная…), естественно, закон сохранения энергии относится и к другим видам энергии.

Если в замкнутой системе действуют неконсервативные силы (трения, например), связанные с потерей энергии, работа неконсервативной силы запишется: А _н.к. = Е ₂ – Е ₁. Работа неконсервативных сил, отрицательная; действие такого рода сил приводит к превращению механической энергии в тепловую энергию.

Рис. 2.9.

Механическая работа, являясь количественной характеристикой превращения одних форм движения в другие, в частности, может быть представлена через увеличение кинетической энергии: DА = ; или уменьшение, если средство передвижения, например, приближается к препятствию. В разделе 2.1. было введено понятие импульса: . Совершённая работа может быть представлена выражением: DА = . Естественно возникает вопрос, что происходит с импульсом системы тел при взаимодействии, поскольку величина силы определяется быстротой (скоростью) изменения импульса тела: . Для простоты возьмём систему, состоящую из трёх тел (рис. 2.9.). Обозначим символами , , результирующие всех сил, с которыми внешние тела воздействуют соответственно на первое, второе и третье тела системы. В то же время, каждой из внутренних сил системы по третьему закону Ньютона соответствует противоположно направленная ей сила; например, силе , с которой на тело 2 воздействует тело 3, соответствует сила , с которой тело 2 воздействует на тело 3; = – (рис. 2.9.). Напишем для каждого из трёх тел второй закон Ньютона через изменение импульса:

Сложим все уравнения вместе. Сумма внутренних сил системы равна нулю, а скорость изменения её импульса: . Что это значит? При отсутствии воздействия внешних тел на систему, изменение импульса системы 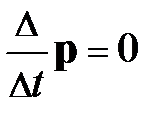, что возможно, если импульс системы не изменяется. Это и составляет суть закона сохранения импульса: в замкнутой системе материальных тел импульс системы до взаимодействия равен импульсу системы после взаимодействия.

Из предыдущего следует, в потенциальном поле каждой точке с одной стороны соответствует некоторое значение силы , с другой стороны, некоторое значение потенциальной энергии. Естественно ожидать, между силой и энергией существует определённая связь. Для установления её вычислим элементарную работу DА, совершаемую силами поля при малом перемещении тела D х: DА = ×D х, где – величина силы на направление перемещения тела х; например, падение тела в поле силы тяжести. Поскольку работа совершается за счёт запаса потенциальной энергии, она равна убыли потенциальной энергии – D П, взятой с противоположным знаком на пути D х: DА = – D П = – (П ₂ – П ₁). Сопоставляя уравнения работы, получаем: ×D х = – D П, откуда следует ; здесь – часто встречающееся в литературе обозначение изменения потенциальной энергии. Таким образом, среднее значение силы на отрезке D х равно быстроте изменения потенциальной энергии, взятой с противоположным знаком.

Отсюда следует важный для нас вывод, который состоит в следующем. Поскольку в замкнутой системе полная энергия остаётся постоянной, то кинетическая энергия может возрастать только за счёт уменьшения потенциальной энергии. Если потенциальная энергия системы имеет минимальное значение, а скорости тел равны нулю, то без воздействия извне тела системы не могут прийти в движение; система находится в равновесии. Таким образом, замкнутая система находится в равновесном, устойчивом состоянии, если её потенциальная энергия соответствует минимальному значению. Из математики известно, для нахождения минимума функции необходимо взять первую производную: и приравнять её к нулю; работая в физике, функциональную зависимость нужно знать или установить её. Если это удалось сделать, можно выявить условие устойчивого равновесия системы.

Для справки. Законы сохранения энергии и импульса получены на основе законов Ньютона. Они являются результатом обобщения экспериментов с упругими, гравитационными и кулоновскими взаимодействиями. В то же время для микромира известны силы ядерного и слабого взаимодействия. Законы сохранения справедливы и для этих взаимодействий. Оказалось, что в основе законов сохранения лежит принцип симметрии пространства–времени. Так, из однородности пространства вытекает закон сохранения импульса, а из однородности времени – закон сохранения энергии; позднее мы узнаем, что из условия изотропности трёхмерного пространства следует закон сохранения момента импульса.

Завершая экскурс в раздел динамики «Законы сохранения в механике. Условия равновесия», перечислим его ключевые слова: закон сохранения энергии для замкнутых и незамкнутых систем, условие равновесия системы, закон сохранения импульса для замкнутых систем.