Математическая запись второго закона динамики позволяет определить величину движущей силы, массы и ускорения не только для текущего момента времени, но и для будущего или предыдущего. В ней говорится о силе как о некоторой мере взаимодействия тел, не вдаваясь в её происхождение. Рассмотрим некоторые конкретные разновидности сил, широко представленные в природе и технике и играющие важную роль в механических процессах.
Под действием силы притяжения к Земле все тела падают с одинаковым, относительно поверхности Земли, ускорением g. Это означает, на всякое тело массы m вблизи Земли действует сила тяжести 
. Если тело покоится относительно поверхности Земли, сила тяжести (m × g) уравновешивается силой реакции 
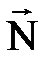подвеса или опоры, и эти силы удерживают тело от падения. По третьему закону Ньютона тело в этом случае действует на подвес или опору с силой 
. Сила, с которой тело действует на подвес или опору, называется весом тела. Очевидно, эта сила равна силе тяжести лишь в том случае, если тело и опора (подвес) не участвуют в ускоренном движении (например, лифт). В противном случае 
. Знак «+» соответствует а с – ускорению системы, направленному вверх, знак «–» – направлению а с вниз (отобразите это на рисунке и с уравнениями).
Закон взаимного притяжения тел (Земля-тело, и не только эта пара) был установлен Ньютоном. Аналитическая запись силы взаимного притяжения (закона всемирного тяготения) имеет вид: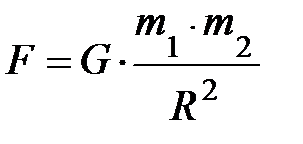 
, где G – постоянная всемирного тяготения, равная 6,67×10–11 м3/кг×с2; m 1 и m 2 – массы взаимодействующих тел; R – расстояние между ними.
Масса, характеризующая инертные свойства тела и масса тела, характеризующая его гравитационные свойства тождественны, что доказано многочисленными опытами. Тождественность инертной и гравитационной масс положена Эйнштейном в основу общей теории относительности.
Весьма распространённым взаимодействием тел является трение. Сила, препятствующая скольжению соприкасающихся тел друг относительно друга, называется силой трения. Она направлена по касательной к поверхности соприкосновения тел противоположно скорости скольжения движущегося тела (отобразили на рисунке?). Естественно ожидать, трение существует и в случае неподвижных относительно друг друга тел – трение покоя. Максимальная сила трения покоя всегда несколько больше силы трения скольжения (в спомните свои ощущения, когда в детстве возили саночки). Таким образом, равномерное прямолинейное движение тела возможно только тогда, когда сила трения скольжения уравновешена движущей, внешней силой.
Трение обусловлено шероховатостью соприкасающихся поверхностей – взаимным зацеплением выступов на них. При достаточно гладких поверхностях главной причиной трения становятся силы межатомного взаимодействия трущихся поверхностей. В механике такого рода силы принято отображать через макропараметры. Для силы трения таким макропараметром является коэффициент трения m. Величина сила трения скольжения не зависит от площади соприкосновения трущихся тел и определяется лишь величиной силы нормального давления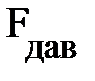 
, прижимающей трущиеся поверхности друг к другу: 
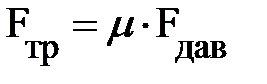(рис. 2.1.). Сила давления не всегда определяется силой тяжести. На рис. 2.1. она равна алгебраической сумме сил – силы тяжести mg и 
, являющейся вертикальной составляющей силы тяги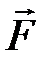 
; 
.
В отличие от сухого вязкое трение характерно тем, что сила вязкого трения обращается в нуль одновременно со скоростью. Поэтому даже малая по величине внешняя сила может сообщить относительную скорость слоям вязкой жидкости. При сравнительно небольших скоростях сила вязкого трения может быть записана в виде: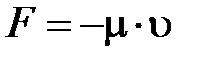 
, где m – коэффициент, зависящий от формы и размеров тела и вязких свойств среды, 
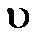– скорость движущегося тела в среде.
Ещё одной силой в механике, возникающей при непосредственном контакте тел, является сила упругости. Здесь результатом взаимодействия является деформация тела; изменение его размеров или формы. Каждое из этих проявлений силы может быть использовано для её измерения.
Деформация тела является упругой, если после снятия нагрузки полностью исчезает. Характер деформации зависит как от величины и длительности действия нагрузки, так и от материала, из которого изготовлено тело. Поэтому силовые (несущие) конструкции изготавливают так, чтобы они работали в области упругих деформаций.
Практика подсказывает, чем большую деформацию мы желаем создать, тем большее усилие нужно приложить к деформируемому телу. Вспомнили ощущения, когда отрывали нить для того, чтобы заштопать рваную дырку; или отломить веточку от куста, чтобы выкопать червяка для рыбалки. Следовательно, абсолютная величина упругой деформации пропорциональна приложенной силе; это и составляет суть содержания закона Гука: 
. Здесь F – приложенная сила,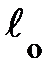 
– первоначальная длина тела, 
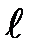– длина деформированного тела, k – коэффициент жёсткости, 
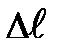– величина упругой деформации; как правило, предельное относительное удлинение упругого характера не превосходит 0,001 межатомных расстояний.
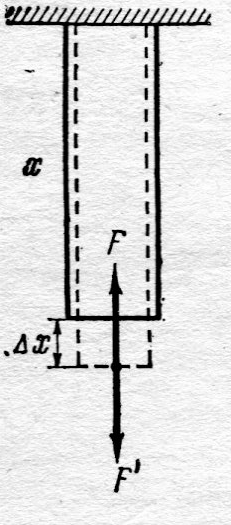
| Рис. 2.2. |
| l |
| Dl |
В продолжение сказанному можно ввести и характеристику упругих свойств твёрдого тела, например, стержня. Будем рассуждать так. Пусть к нижнему концу стержня длиной 
и площадью поперечного сечения S приложена деформирующая сила 
(рис. 2.2.). Стержень удлиняется (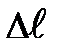
) и в нём возникает сила упругости F = – . Опыт показывает, удлинение 
пропорционально деформирующей силе, первоначальной длине стержня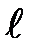 
, обратно пропорционально площади его поперечного сечения S и зависит от упругих свойств вещества E, из которого сделан стержень: 
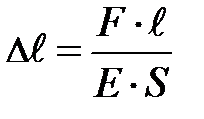. Здесь величина Е, называемая модулем Юнга, зависит от внутренней структуры вещества стержня. Если относительное удлинение 
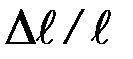обозначить через e, а отношение F / S = s, сила, приходящаяся на единицу площади и называемая нормальным механическим напряжением, то 
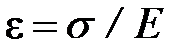. Таким образом, относительное удлинение стержня тем меньше, чем больше модуль Юнга вещества Е.
Приведём несколько примеров, иллюстрирующих физическое содержание основного закона механики: геометрическая сумма сил, действующих на тело, равна произведению массы тела на ускорение и направлена вдоль ускорения. С помощью основного закона динамики можно определить силы, действующие на тело, или по заданным силам – уравнение движения тела. Рассмотрим силы, которые действуют на груз, лежащий на полу лифта, движущемся с ускорением вертикально вверх (рис. 2.3.). На груз действует сила со стороны Земли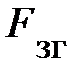 
(mg) и со стороны дна лифта сила реакции дна лифта 
. Поскольку груз движется вверх, естественно,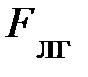 
> 
. Учитывая, что равнодействующая сила совпадает с направлением ускорения, то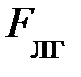 
– 
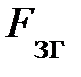= m × a. Так как 
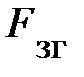= mg, то 
= mg + m × a. Взаимодействие груза с лифтом есть не что иное как сила, с которой груз давит на дно лифта 
. Следовательно, сила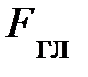 
является весом тела. Аналитическая запись примет вид: 
= P = mg + m × a; см. рис. 2.3.. Отсюда следует, вес тела, сила взаимодействия груза с подставкой, «чувствительна» к направлению движения и может быть равна силе тяжести, больше силы тяжести или меньше её. Из последнего равенства следует ещё один вывод. Если ускорения а и g равны по величине, но противоположны по направлению, вес тела равен нулю; состояние невесомости. Сейчас можно вернуться ко второму абзацу данного параграфа и решить обозначенную в нём задачу. Попробуйте.
| Рис.2.3. |
|
|
|
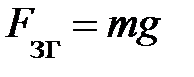
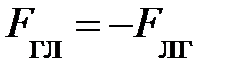
, развиваемую автомобилем. Поскольку автомобиль взаимодействует с Землёй, на него действует сила тяжести mg (рис.2.4). Составляющая силы тяжести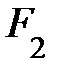 
является силой нормального давления автомобиля на наклонную плоскость P; из прямоугольного треугольника сил 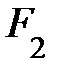= P = m×g× cosa и определяет силу сопротивления движению 
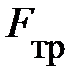= m×P. В то же время, составляющая силы тяжести на направление движения 
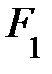препятствует поступательному движению автомобиля вверх и из треугольника сил 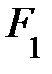= m×g× sina. По второму закону Ньютона 
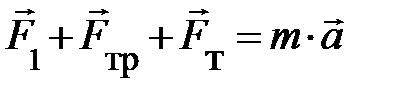. В скалярной форме, принимая за положительное направление оси отсчёта направление движения автомобиля (направление 
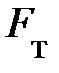) см. (рис.2.4), уравнение динамики примет вид: 
. Подставляя заданные величины, после несложных преобразований можно выразить силу ; разумеется, в общем виде; проделали? Численный результат зависит от заданных величин. Задачу можно переформулировать, например, задаться вопросом: «каким должен быть минимальный коэффициент трения (колесо–Земля), чтобы автомобиль смог подняться в гору?». При движении автомобиль «отталкиваться» от Земли, если возникает достаточная сила трения. Заметим, здесь не отображена сила реакции N (отобразите).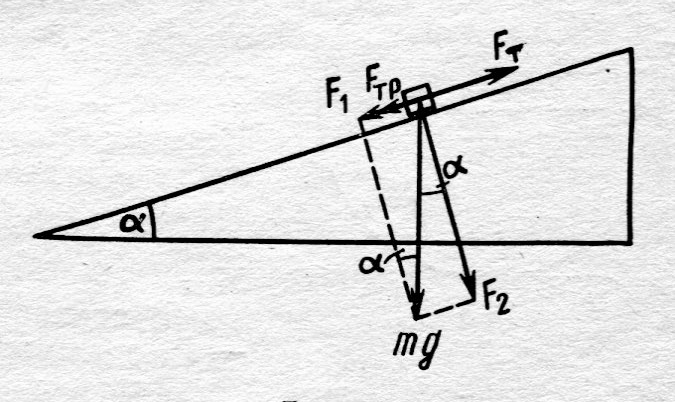
| Рис. 2.4. |
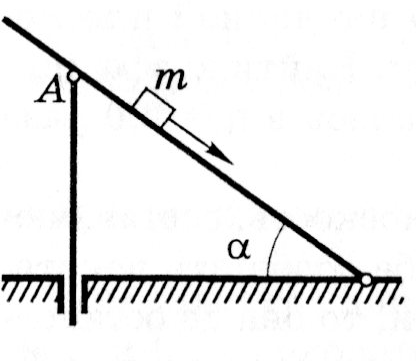
| Рис. 2.5. |
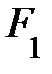, составляющая силы тяжести на направление наклонной плоскости, обеспечивающая скольжение тела; сила 
, препятствующая движению тела вниз. Не забудьте, сила трения обеспечивается составляющей силы тяжести, перпендикулярной к наклонной плоскости. Записав второй закон динамики в скалярной форме, можно найти ускорение скольжения тела m по наклонной плоскости. Во-вторых, задача поднимает вопросы из кинематики. При составлении уравнений кинематики придётся вводить величины, которые не заданы, например, путь скольжения. 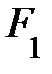Потребуется ускорение, которое обусловлено силами , , время t; основание наклонной плоскости b задано. Далее задача переводится в исследовательскую плоскость математики, выполнение математических действий, подготавливающих уравнение движения к поиску условия минимума для времени t. Очевидно, потребуется найти аналитическую зависимость времени соскальзывания тела с наклонной плоскости через заданные величины. Сформулированный в условии задачи вопрос предполагает, время должно быть выражено через заданные величины, и, в частности, через a: t = f (a). Осталось определить, какую математическую операцию необходимо выполнить, чтобы найти условие минимума. В математике неизвестная величина, как правило, обозначается символом х, в условии предложенной задачи a, с точки зрения математики a = х. Возможно, эта запись облегчит выполнение математической операции при нахождении минимума времени соскальзывания. Удачи.
Завершая экскурс в раздел динамики «Силы в механике. Практическое применение закон Ньютона» перечислим его ключевые слова: сила тяжести, вес тела, сила реакции, сила упругости, сила трения, макропараметр силы упругости и трения.
