Задание 1
1. Вычислите частоту колебаний релаксационного генератора:
(8.33)
Результаты вычислений занесите в таблицу I.
2. Постройте график зависимости периода колебаний релаксационного генератора То от напряжения питания: 
.
Задание 2
1. Вычислите значения отношения амплитуд: 
и логарифмического декремента затухания для каждого значения сопротивления по формуле
(8.34)
Результаты вычислений занесите в таблицу 8.2.
2. Вычислите значения добротности Q по формуле (8.28). Результаты вычислений занесите в таблицу 2.
3. Вычислите значение частоты затухающих колебаний по формуле (8.33).
4. Постройте график зависимости добротности Q от сопротивления R: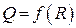 
.
5. Для слабого затухания логарифмический декремент затухания зависит от активного сопротивления контура линейно:
(8.35)
(ср. с формулой (8.26), где RL - активное сопротивление катушки индуктивности.
Обозначив 
, 
, (8.36)
получим 
. (8.37)
Неизвестные коэффициенты а и b линейной зависимости (8.37) найдите методом наименьших квадратов. Для этого вычислите суммы вида:
, 
, 
, 
, 
Результата вычислений занесите в таблицу 8.3.
Таблица 8.3 – Метод наименьших квадратов
| контур | ΣRi | ΣRi2 | Σλi | Σλi2 | ΣλiRi | a | b | ∆a | ∆b | RL, Ом | ∆RL, Ом | L, Гн | ∆L, Гн | C, Ф | ∆C, Ф |
| L, C |
По формуле (8.18) методических указаний "Введение в теорию погрешностей" вычислите значение коэффициентов а, b по формулам (8.20), (8.21) – погрешности ∆a, ∆b. Результаты вычислений занесите в таблицу 8.3.
6. Постройте график зависимости λ = λ(R). При этом нанесите на график значения λ; R в экспериментальных точках, а прямую проведите согласно уравнению (8.37) с рассчитанными коэффициентами а, b.
7. Определите активное сопротивление катушки индуктивности RL по формуле
, (8.38)
8. Период колебаний Т определяется по формуле
(8.39)
(ср. с формулой 8.16).
Для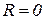 
(из табл. 8.2) (8.40)
Из (8.38), (8.40), (8.42) следует: 
.
Отсюда получаем формулы для определения индуктивности L и емкости С контура:
(8.41)
(8.42)
По значениям периода Т1 затухающих колебаний при R = 0, коэффициентов а, b вычислите индуктивность L и емкость С контура по формулам (8.41), (8.42).
Результаты вычислений занесете в таблицу 8.3.
9. Вычислите относительные погрешности:
(8.43)
(8.44)
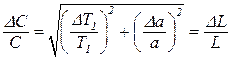(8.45)
∆Т1 - длительность развертки, соответствующая 1 мм.
10. Вычислите абсолютные погрешности ∆RL, ∆L, ∆С. Результаты вычислений занесите в таблицу 3.
11. По формуле (8.39) для каждого значения сопротивления R вычислите теоретически ожидаемое значение периода Ттеор. Результаты вычислений занесите в таблицу 8.2.
12. Округленные результаты запишите в интервальной форме:
, 
, 
.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как возникают колебания в колебательном контуре?
2. Выведите и решите, уравнения свободных незатухающих и затухающих колебаний в колебательном контуре.
3. Как зависит период затухающих колебаний от сопротивления контура? Что такое критическое сопротивление?
4. Как изменяется со временем напряжение на конденсаторе, сила тока в контуре, энергия электрического и магнитного полей?
5. Что такое постоянная времени затухания и логарифмический декремент затухания?
6. Чему равен логарифмический декремент затухания колебательного контура?
7. Что называется добротностью? Ее физический смысл.
8. Принцип работы релаксационного генератора на газоразрядной лампе.
9. Как изменяется период колебаний релаксационного генератора с ростом напряжения и почему?
10. Принцип получения затухающих колебаний на экране осциллографа в данной работе.
11. Как измерить период колебаний с помощью осциллографа?
12. Почему колебания в контуре установки являются затухающими даже при активном сопротивлении R = 0?
ЛИТЕРАТУРА [1, с. 243-247], [3, с. 253-280], [4, с. 158-170]
ЛАБОРАТОРНАЯ РАБОТА № 3.9
ИССЛЕДОВАНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Цель работы: Изучение вынужденных колебаний в последовательном колебательном контуре; снятие его резонансных характеристик (амплитудочастотных и фазочастотных); определение добротности, контура, параметров его элементов (индуктивности, ёмкости, активного сопротивления).
Материалы и оборудование: Наборы неизвестных конденсаторов, катушек индуктивности, сопротивлений; генератор сигналов ГЗ-35; частотомер электронносчетный 43-34А; вольтметр; осциллограф.
Практическое значение: вынужденные колебания используются в радиотехнике при приеме и настойке на определенную частоту радиосигнала; явление резонанса широко используются в измерительной технике, телеуправлении, различных схемах автоматики, рентгеноскопии, для изменения (компенсации) параметров электропередач, повышает коэффициенты мощности нагрузки.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1. Чтобы в колебательном контуре, электрическая схема которого представлена на рис. 9.1, совершились вынужденные колебания, необходимо включить последовательно с элементами контура генератор – источник ЭДС. ε:
(9.1)
По закону Ома для неоднородного участка цепи имеем для контура (потенциал обкладок и направление тока показаны на рис. 9.1; направление обхода – по часовой стрелке):
, (9.2)
где 
– ЭДС самоиндукции; активное сопротивление катушки индуктивности включено в R; внутренним сопротивлением генератора пренебрегаем.
Пусть q – заряд на обкладках конденсатора, тогда: 
; 
и получаем уравнение вынужденных колебаний:
(9.3)
Обозначая 
, 
, (9.4)
где ω0 – собственная частота контура, β – коэффициент затухания, получаем:
(9.5)
(точка обозначает дифференцирование по времени).
Уравнение (9.5) является неоднородным линейным дифференциальным уравнением второго порядка. Такого типауравнения описывают поведение широкого класса колебательных систем (электрических, механических) под влиянием внешнего синусоидального воздействия.
Общее решение уравнения (9.5) складывается из общего решения q1 однородного уравнения:
(9.6)
и частного решения неоднородного уравнения (9.5). Общее решение однородного уравнения (9.6), в случае слабого затухания 
, описывает собственные затухающие колебания:
, (9.7)
где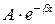 
– амплитуда колебаний; 
– циклическая частота затухающих колебаний. Константы А и α из начальных условий.
Частное решение уравнения (9.5) проще всего искать в комплексной форме, сделав замену в правой части 
.
Правая часть уравнения (9.5) пропорциональна действительной части этого выражения. Пусть решением нового уравнения является комплексная функция 
, так что
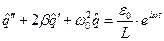. (9.8)
Тогда действительная часть функции Re является решением уравнения, у которого в правой части стоит 
,т.е. искомым решением уравнения (9.5).
Будем искать частное решение уравнения (9.8) в виде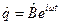 
. Подставляя это выражение в уравнение (9.8) получим: 
, тогда
.
Обозначим 
и запишем знаменатель 
в показательной форме 
, где ρ – модуль 
; ψ – фаза р определяются выражениями:
; (9.9)
; (9.10)
Тогда 
, 
(9.11)
И частное решение q 2 уравнения (9.5) определяется формулой:
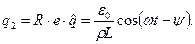. (9.12)
Общее решение уравнения (9.5) запишем в виде:
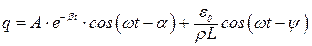(9.13)
Формула (9.13) показывает, что при воздействии на контур синусоидальной ЭДС, в нем возникают колебания двух частот:
– вынужденные незатухающие колебания с частотой внешней ЭДС (второй член уравнения);
– затухающие колебания с собственной частотой ωi.
Амплитуда собственных колебаний 
зависит от начальных условий и от времени. С течением времени она становится пренебрежительно малой по сравнению со вторым членом уравнения (9.13), и в контуре устанавливаются вынужденные колебания. Процесс установления вынужденных колебаний называется переходным. В дальнейшем будем полагать, что переходные процессы закончились и 
. В установившемся режиме заряд на конденсаторе изменяется по закону:
(9.14)
; (9.15)
(9.16)
Сила тока в контуре меняется по закону:
(9.17)
Здесь 
– сдвиг фаз между током в контуре и приложенной внешней ЭДС. Амплитудное значение тока I0 и сдвиг фаз рассчитываются по формулам:
; (9.18)
. (9.19)
Величины 
и 
называются реактивными индуктивным и емкостным сопротивлениями соответственно, а
(9.20)
определяет полное сопротивление цепи или импеданс (или точнее его модуль).
Таким образом, между амплитудными значениями силы тока I 0 и ЭДС существует соотношение 
– аналог закона Ома для постоянного тока.
Сдвиг фаз φ в цепи определяется соотношением активных и реактивных сопротивлений:
- если в контуре присутствует только активное сопротивление, φ = 0 (ток колеблется в одной фазе с приложенной ЭДС);
- если в контуре присутствует только индуктивное сопротивление 
(ток отстает по фазе на 
от приложенного напряжения);
- если в контуре присутствует только емкостное сопротивление 
(ток опережает по фазе на приложенную ЭДС).
Сумма падений напряжений в последовательном контуре равна внешней ЭДС:
, (9.21)
где падения напряжения на каждом из элементов цепи определятся соотношениями:
(9.22)
(9.23)
(9.24)
 |
Соотношение между амплитудными значениями падений напряжения выглядят следующим образом:
; 
; 
. (9.25)
Фазовые соотношения между 
, 
; 
легко представить в виде векторной диаграммы, приведенной на рис. 9.2.
2. Явление резкого возрастания амплитуды вынужденных колебаний при приближении их частоты к некоторой характерной для данной колебательной системы частоте – называется резонансом.
Найдем частоту ω внешней ЭДС, при которой сила тока в контуре максимальна. Из формулы (9.18) следует, что I0 достигает максимума, когда 
, т. е. резонансная частота для тока определяется выражением:
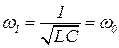, (9.26)
т.е. совпадает с собственной частотой свободных колебаний контура и не зависит от активного сопротивления. При этом
(9.27)
,
,
т.е. 
и все приложенное внешнее напряжение падает на активном сопротивлении. Это явление называется резонансом напряжений.
При 
сдвиг фаз между силой тока в контуре и внешней ЭДС равен нулю: 
, 
т. е. контур ведет себя, как активное сопротивление. Зависимость амплитудных значений тока, напряжения в контуре от частоты носит название резонансной кривой. Резонансная кривая для тока в контуре описывается уравнением (9.18) и изображена на рис.9.3.
На рис. 9.3 видно, что все резонансные кривые начинаются в нуле и максимум кривой тем выше и острее, чем меньше коэффициент затухания β, т.е. чем меньше активное сопротивление и больше индуктивность (такой же вид имеют резонансные кривые для напряжения на активном сопротивлении)
Амплитуда напряжения на конденсаторе 
зависит от частоты следующим образом:
(9.28)
Максимального значения амплитуда достигает тогда, когда выражение 
– минимально. Для нахождения этой частоты возьмем производную от него по ω и приравняем ее к нулю: 
. Тогда резонансная частота для напряжения на конденсаторе определится выражением:
(9.29)
Резонансная частота 
меньше собственной, причем это отличие тем больше, чем больше затухание в контуре
На рис. 5 изображено семейство резонансных кривых для напряжения на конденсаторе в последовательном контуре. При 
все кривые начинаются в точке 
. Максимальное значение 
:
 |
3. Важной характеристикой колебательного контура является добротность Q. Это безразмерная величина, характеризующая относительную величину потерь энергии в контуре:
, (9.31)
где W – энергия контура в данный момент, ΔW – убыль энергии за период.
Добротность связана с логарифмическим декрементом затухания:
, (9.32)
где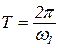 
– период затухания колебаний.
(9.33)
В случае слабого затухания 
. В этом случае резонансное напряжение на конденсаторе (в случае слабого затухания не делается различие между 
и 
) равно:
, (9.34)
т.е. добротность показывает во сколько раз резонансная амплитуда напряжения на конденсаторе контура больше амплитуды приложенной ЭДС.
Добротность можно определить по резонансной кривой. Определим ширину резонансной кривой следующим образом: проведем горизонтальную прямую 
и найдем частоты 
и 
в точках пересечения её срезонансной кривой (рис.9.6).
определяется по формуле (9.28), а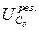 
– по формуле (9.30).
Поскольку по построению,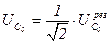 
то получаем уравнение для определения и 
:
, (9.35)
решение которого выглядит следующим образом: 
.
Обозначив эти решения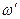 
и , получим: 
.
Для не очень большого затухания
, 
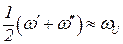. (9.36)
Тогда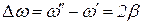 
(9.37)
и добротность определяется следующим образом:
, (9.38)
т.е. добротность равна отношению частоты к ширине резонансной кривой.
Точно таким же образом определяется добротность по резонансной кривой для силы тока: 
. (9.39)
4. Резонансные характеристики контура можно использовать для определения параметров его элементов. Реальный контур отличается от идеализированного (рис. 9.1) тем, что катушка индуктивности L имеет активное сопротивление RL и, измеряя напряжение на катушке, мы тем самым измеряем суммарное падение напряжения на индуктивности и активном сопротивлениях (рис. 9.7).
Пусть сила тока при резонансе напряжений равна 
. Тогда падение напряжения (амплитудные значения) на элементах контура определится соотношениями:
, 
, 
(9.40)
(они выполняются для любых частот). Отношения напряжений равны
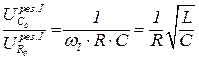(9.41)
(9.42)
(использовано соотношение 
).
Решая эти уравнения относительно R, C, L (c использованием определения ), получаем:
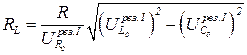, (9.43)
, (9.44)
, (9.45)
где 
- частота резонанса для силы тока.
Формулы (9.43 ÷ 9.45) используются для нахождения параметров элементов цепи. Активное сопротивление можно вычислить, зная ток в цепи и падение напряжения на R:
(9.46)
Амплитуды напряжения на конденсаторе достигают максимального напряжения 
на частоте: 
. (9.47)
Выразим добротность Q контура через и :
(9.48)
(см. формулу 9.33)
; 
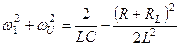. (9.49)
Решая (9.48)) ÷ (9.49), получаем: 
. (9.50)
При 
амплитуда напряжения на конденсаторе: 
. Так как при слабом затухании добротность определяется по формуле:
, (9.51)
то 
, где ε0 - амплитуда ЭДС генератора.
ОПИСАНИЕ УСТАНОВКИ
Электрическая схема установки приведена на рис 9.8. Требуемые элементы последовательного колебательного контура выбираются с помощью переключателей (L1 - L4,; С1 – С5, R1- R6). Контур подключается к выходу 2 генератора сигналов ГЗ-З5. К выходу 1 генератора подключается вход А электронносчетного частотомера 4З-34А. Последовательно с элементами контура включено сопротивление R=1 Ом так, что падение напряжения на нём численно равно силе тока в цепи. Его включение вызвано тем, что сила тока измеряется цифровым вольтметром по падению, напряжения. Подключение вольтметра к катушкам индуктивности, конденсаторам, активным сопротивлениям и резистору R осуществляется переключателями, расположенными вблизи клемм подключения вольтметра.
Сдвиг фаз между силой тока в контуре и приложенной ЭДС измеряется с помощью осциллографа. На горизонтальный вход X осциллографа подаётся сигнал с генератора, уровень которого регулируется потенциометром Rус. (регулятор «Усиление X» расположен на стенде). На вертикальный вход У осциллографа подаётся напряжение, падающее на активном сопротивлении контура, пропорциональное силе тока в цепи. Таким образом, на электронный луч действуют две колеблющиеся во взаимно-перпендикулярных направлениях силы. Рассмотрим траекторию луча, получающуюся при сложении двух взаимно-перпендикулярных колебаний.
; 
(9.53)
;
; 
.
Отсюда, исключая время t, получаем уравнение траектории:
(9.54)
 |
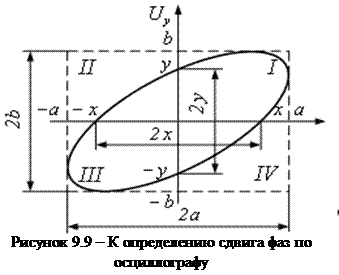Это уравнение эллипса. Ориентация эллипса зависит как от искомого сдвига фаз φ, так и от усиления каналов Х и У. При. 
эллипс вырождается в прямую, пересекающую 1 и 3 квадранты экрана осциллографа. При увеличении или уменьшении φ эллипс становится более или менее "полным", но он всегда будет вписан в прямоугольник со сторонами 2а и 2в (рис. 9.9).
При 
из (9.54) получаем 
; при 
: 
.Измеряя размеры эллипса 2а, 2b и координаты точек его пересечения с осями х, у, определяем 
.Тогда
(9.55)
Положительные и отрицательные значения на картинке неотличимы. Эти значения отличаются друг от друга не видом картинки, а направлением движения луча, которое на обычном осциллографе не определится. Размеры эллипса 2а или 2в следует измерять при выключенном усилении У или X, когда эллипс вырождается в отрезок горизонтальной или вертикальной прямой.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Соберите схему.
2. Выход 1 генератора Г3 - 35 подключите ко входу А частотометра 43-34А, выход П генератора и клемму «
» подключите к клеммам, на стенде.
3. Переключатель " Метки времени " частотомера поставьте в положение «→)А», переключатель «Время измерения» – в положение " I S ", переключатель " Род работы " – частоты А, Б; переключатели расположенные слева и справа от входа А переведите, в положение " 1:1 " и «~» соответственно.
4. Переключатель длительности развертки осциллографа переведите в положение " ВходX ".
5. Включите приборы и дайте им прогреться в течение 5 минут.
6. Переключатель " Пределы шкал " генератора ГЗ-35 поставьте в положение " 10 V ", а ручкой " Peг. вых. напр. " установите по вольтметру генератора на напряжение 5 B.
7. Отключите входы X и У осциллографа и ручками «
» и «
»установите светящееся пятно в центр координатной сетки. Подключите входы осциллографа к соответствующим клеммам на стенде. Тумблер " X " поставьте в. положение " ВКЛ ".
8. Выберите переключателями элементы контура L, C, R, указанные преподавателем.
9. Подключите цифровой вольтметр к клеммам на стенде. Переключатель рода работы на стенде поставьте в положение 
.
10. Ручками " Усиление X " на стенде и регулятором " Усиление " осциллографа добейтесь, чтобы изображение эллипса занимало большую часть экрана.
11. Ручками " Частота " и переключателем " Множитель " генератора ГЗ-35 получите изображение прямой (вырожденного эллипса) на экране осциллографа. При необходимости измените усиление осциллографа.
12. Прямая на экране осциллографа соответствует нулевому сдвигу фаз между током и приложенной ЭДС, т.е. резонансной частоте для силы тока. Более точно резонанс определится по напряжению на сопротивлении R, измеряя напряжение вольтметром.
При этом выберите предел измерения, обеспечивающий максимальную чувствительность (мигающий символ " П " в первом разряде означает переполнение – перейдите на следующий предел).
13. Измеренное частотомером значение резонансной частоты для силы тока 
и соответствующее напряжение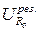 
занесите в таблицу 9.3. Эту же частоту и напряжение на сопротивлении занесите в графы ν и 
таблицы 9.1. Подключите вольтметр к клеммам " генератор " на стенде и измерьте напряжение на них - εо. Результат занесите в таблицу 9.3, а вольтметр верните в исходное положение.
14. Переключателями на стенде подключите вольтметр поочередно к конденсатору и катушке индуктивности. Измеренные значения напряжении 
и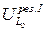 
занесите в таблицу 3. Переключателем на стенде подключите вольтметр к активному сопротивлению.
15. Тумблер " X " на стенде поставьте в положение " Выкл ". Измерьте высоту вертикальной линии 2b на экране осциллографа. Переведите тумблер в положение. " Вкл " и измерьте "толщину" эллипса 2у (рис. 9.9) (для прямой 2у = 0), Результаты занесите в таблицу 9.1.
16. Уменьшая частоту генератора так, чтобы амплитуда напряжения на сопротивлении уменьшалась каждый раз на 10% от максимальной, снимите 7–8 значений напряжения 
. В каждой точке измеряйте. параметры 2в и 2у эллипса на экране осциллографа согласно п.14. Получаемые значения 2в, 2у и частоты ν заносят в таблицу 9.1.
17. Вернувшись к резонансной частоте повторите измерения по п.16, увеличивая частоту генератора. Измеренные в 7-8 точках значения; , ν, 2в, 2у занесите в таблицу 9.1.
18. Переключателем на стенде подключите вольтметр В7-27А/1 к конденсатору. Изменяя частоту генератора, добейтесь максимума напряжения на конденсаторе (соответствующая резонансная частота 
и будет меньше резонансной частоты 
). Значение, резонансной частоты занесите в таблицу 9.3. Эту же частоту вместе со значением напряжения Uc0 занесите в таблицу 9.2.
19. Уменьшая частоту от до20 Гц снимите7- 8 значений напряжения на конденсаторе Uc0. Результаты измерений Uc0 частоты ν занесите в таблицу 9.2.
20. Увеличивая частоту от 
так, чтобы амплитуда напряжения на конденсаторе Uc0 уменьшалась на 10% от максимальной, снимите ещё 7-8 точек резонансной кривой; Результаты занесите в таблицу 9.2.
Таблица 9.1 –Резонанс силы тока и сдвиг фаз между током и напряжением
| № п/п | Контур 1 | ν (Гц) |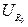 
(В)
| 2b (мм) | 2у (мм) | φ (мм) |
| . . . | Li Cj Rk |
Таблица 9.2 – Резонанс напряжения на конденсаторе
| № п/п | Контур 1 | ν (Гц) | 
(В)
|
| . . . | Li Cj Rk |
Таблица 9.3 – Резонансные характеристики и параметры контура
| Контур Li Cj Rk | ν I Гц | 
B
| 
В
|  В
|  ,
Гц
| νu, Гц | I0 мА | U0 B |
| B Ом | RL Ом | C мкФ | L Гн | Q1 | Q2 | Q3 | Q4 | Q5 |
21. Не изменяя выбранного сопротивления R,включите в контур катушку L1 и конденсатор С5. Найдите резонанс по картинке на осциллографе. Измерьте напряжение на сопротивлении U0. Измерьте силу тока в контуре 
(нажав клавишу 1 на стенде) вольтметром (при этом напряжение на Rш в милливольтах численно равно току I0 в миллиамперах). Результаты занесите в таблицу 9.3.
22. Повторите пункты 11-21 задания с двумя другими значениями активного сопротивления (не изменяя L, С).
