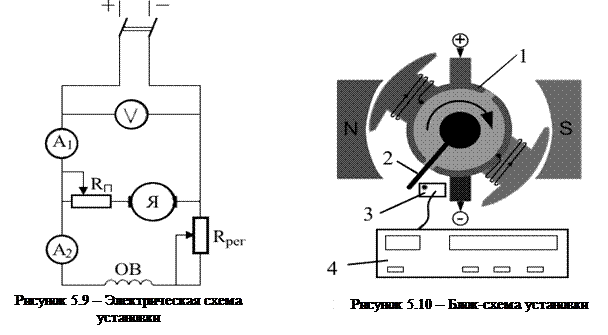
На рис.5.9 представлена электрическая схема установки. Питание двигателя осуществляется источником постоянного тока напряжением 9В. Пуск двигателя выполняется при помощи сопротивления RП. Регулировка тока – реостатом RРЕГ. На валу двигателя (1) на рис. 5.10 прикреплен прерыватель (2), который отсчитывает обороты через фотодатчик (3). В цепь фотоэлемента датчика включено счетное устройство (4) (рис.5.10), позволяющее измерить число и время N-го количество оборотов.
3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Получить у преподавателя разрешение на пуск двигателя. Для пуска двигателя необходимо убедиться, что пусковой реостат RП в цепи якоря должен быть полностью введен, а регулировочный реостат RРЕГ в цепи возбуждения полностью выведен.
2. Включить ключ питания и, постепенно выводя пусковой реостат, пустить в ход двигатель.
3. Снять характеристику холостого хода: n = ƒ (I В).
4. Постепенно вводить реостат в цепь возбуждения с таким расчетом, чтобы скорость двигателя не превысила номинальную.
5. При достижении двигателем постоянной скорости после сброса счетчика оборотов нажать пуск и измерить время 10-20 оборотов.
6. Данные занести в таблицу 5.1
7. Эксперимент повторить три раза для различно числа оборотов.
8. Снять показания (7-8 точек) для различных значений I В. Полученные данные записать в таблицу 5.1.
Таблица 5.1 – Экспериментальные данные
| № | IВ | N | t,c | n i, об/с | n, об/с |
9. По данным опыта построить характеристику холостого хода n = ƒ (I В).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Устройство и принцип действия двигателя.
2. Классификация двигателей.
3. Особенности пуска.
4. Способы регулирования скорости вращения.
5. Саморегулирование двигателя.
6. Реверсирование двигателя.
7. Объяснить характеристики двигателя.
ЛИТЕРАТУРА [1, c.236-241], [2, c.141-148], [3, c.174-177], [4, c.190-201],
ЛАБОРАТОРНАЯ РАБОТА № 3.6
ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА МЕТОДОМ МАГНЕТРОНА
Цель работы: исследование движения заряженных частиц в скрещенных электрическом и магнитном полях; определение отношения заряда электрона к его массе.
Материалы и оборудование: кенотрон (вакуумный диод) В 1-0,1/30, соленоид, блок питания 0–50 В, блок питания цепей накала и соленоида, ЛАТР, амперметр, вольтметр, миллиамперметр.
Практическое значение: магнетроны являются генераторами электромагнитных колебаний и рассчитаны в настоящее время для работы в узкой полосе частот в диапазоне 300 ÷300 000 МГц при выходной мощности в импульсе от 10 Вт до 10 МВт и длительности импульса 0,1÷5 мкс
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1. Отношение заряда электрона, е к его массе т называется удельным зарядом. Для измерения удельного заряда 
применяют различные методы. Все они основываются на том, что характеристики движения заряженных частиц в электрическом и магнитном поле зависят от . Рассмотрим, например, движение положительно заряженной частицы в однородном магнитном поле. Пусть частица влетает в однородное магнитное поле с индукцией В со скоростью v, перпендикулярно силовым линиям смотри рис. 6.1.
Со стороны магнитного поля на частицу действует сила Лоренца:
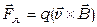, (6.1)
(направление силы показано на рис. 6.1).
Так как 
перпендикулярна 
, то работы она не совершает, следовательно, модуль вектора скорости не изменяется, изменяется лишь его направление. Сила Лоренца, перпендикулярная вектору скорости, является в этом случае центростремительной, а траектория движения частицы – окружность. Для нахождения радиуса окружности запишем второй закон Ньютона:
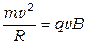, (6.2)
где α – угол между векторами и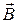 
; в нашем случае 
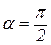; m – масса частицы.
Тогда: 
(6.3)
Период Т обращения частицы по окружности вычислим следующим способом:
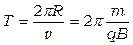(6.4)
Из формул (6.3) и (6.4) видно, что радиус траектории и период обращения зависят от удельного заряда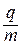 
поэтому измерение этих параметров движения, может быть положено в основу определения .
 |
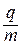Если частица влетает в однородное магнитное поле под углом α к линиям индукции магнитного поля, то траекторией движения будет винтовая линия, (рис. 6.2) – частица участвует в равномерном движении в направлении поля и вращается в плоскости, перпендикулярной полю.
Радиус R витка, шаг спирали h и период обращения вычисляются по формулам:
, 
, 
(6.5)
2. В настоящей работе отношение для электрона определяется с помощью метода, получившего название " метода магнетрона ". Это название связано с тем, что применяемая в работе конфигурация электрического и магнитного полей совпадает с конфигурацией полей в магнетроне – генераторе электромагнитных колебаний СВЧ диапазона. Движение электронов, испускаемых нагретым катодом, вакуумного диода в этом случае, происходит в кольцевом пространстве, заключенном между катодом и анодом двухэлектродной электронной лампы (рис. 6.3). Нить накала – катод – коаксиальна с цилиндрическим анодом, так, что электрическое поле направлено радиально и в силу симметрии зависит только от координаты r цилиндрической системы координат. Сам вакуумный диод помещен внутрь соленоида так, что магнитное поле соленоида В направлено параллельно оси катода, т.е. перпендикулярно электрическому полю. Электрическое поле ускоряет электроны в пространстве между электродами, а магнитное поле искривляет их траекторию, т.е. равнодействующая сила равна векторной сумме
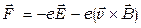, (6.6)
где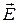 
– напряженность электрического поля; В – индукция магнитного поля.
Под действием такой сложной системы сил электроны движутся по траекториям, показанным на рис.6.4. В отсутствии магнитного поля траектория электрона прямолинейна и направлена вдоль- радиуса.
При слабом магнитном поле траектория несколько искривляется, но электрон все же достигает анода. При некотором критическом значении индукции магнитного поля Вкр траектория искривляется так сильно, что только касается анода. При В > Bкр электрон вовсе не попадает на анод и возвращается к катоду. Траектория электрона в общем случае представляет собой кривую с переменной кривизной, радиус которой увеличивается при приближении к аноду. (Чем больше скорость электрона, тем больше радиус кривизны согласно формуле (6.3)).
Величина критического поля Bкр определяется соотношением
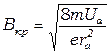. (6.7)
 |
Если определить Bкр, то соотношение может быть использовано для нахождения удельного заряда электрона:
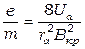. (6.8)
 |
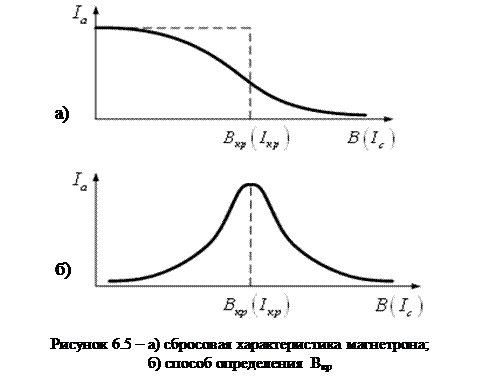Для нахождения Bкр необходимо исследовать зависимость анодного тока Ia от индукции магнитного поля. Если все электроны вылетают с катода с одинаковыми скоростями, то при В < Вкр все они попадают на анод и создают анодный ток, а при B ≥ Bкр электроны на анод не попадают – анодный ток прекращается. Зависимость анодного тока от индукции магнитного поля – сбросовая характеристика – в этом случае показана на рисунке 6.5, а пунктиром. На самом деле электроны, испускаемые нагретым катодом, обладают различными начальными скоростями. Критические условия достигаются, поэтому для различных электронов при различных значениях В. По этой причине, сбросовая характеристика "размазывается". Её вид изображен сплошной линией. Кроме того, к "размазыванию" сбросовой характеристики приводят и другие причины: некоаксиальность анода и катода, наклон вектора магнитной индукции по отношению к катоду и т.д. Все эти причины затрудняют определение Bкр по сбросовой характеристике.
Однако, большая часть электронов вылетает из катода с нулевой начальной скоростью, поэтому при B ≈ Bкр большая часть электронов перестает попадать на анод и скорость уменьшения анодного тока в зависимости от В максимальна. Скорость уменьшения анодного тока равна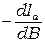 
, поэтому при В=Bкр она имеет максимум (рис. 6.5,б), что позволяет определить поле Вкр, а в эксперименте – соответствующее ему значение критического тока Iкр.
3. Магнитное поле, действующее на электрон в диоде, создается соленоидом – длинной катушкой, внутрь которой помещен вакуумный диод. Длинной называют катушку, для которой l >> D, где l – длина катушки, а D – ее диаметр. Магнитное поле внутри соленоида практически однородно (В = const), а снаружи отсутствует. Для вычисления индукции магнитного поля внутри соленоида используется теорема о циркуляции вектора напряженности Н магнитного поля (закон полного тока):
, (6.9)
т.е. циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов, проходящих через поверхность, натянутую на контур. Сила тока берется со знаком "+", если направление тока совпадает с направлением нормали 
к поверхности, связанным с направлением обхода контура правилом буравчика (рис. 6.6). После преобразований напряженность Н и индукция В магнитного поля внутри длинного соленоида определяются выражениями:
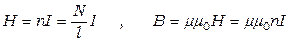, (6.10)
где μ - магнитная проницаемость материала сердечника соленоида.
 |
Индукция магнитного поля внутри длинного соленоида, в который помещен диод, пропорциональна силе тока I в соленоиде, поэтому зависимость анодного тока от тока в соленоиде – сбросовая характеристика – аналогична зависимости Ia(B) (рис. 6.5). Критический ток. в соленоиде Iкр соответствует критическому значению магнитной индукции Вкр и определяется как ток в соленоиде, при котором скорость убывания анодного тока максимальна
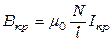. (6.11)
Тогда для определения удельного заряда электрона получаем окончательную формулу:
, (6.12)
где k – коэффициент лабораторной установки, определяющийся ее параметрами
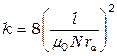. (6.13)
Значения этих параметров:
N = 8400 – число витков соленоида;
l = (24,5 ± 0,5) см - длина соленоида;
r a = (5,5 ± 0,1) мм – радиус анода.
