1. Для нахождения критического тока Iкр необходимо продифференцировать сбросовую характеристику Ia = f(Ic). Дифференцирование выполняется численным методом.
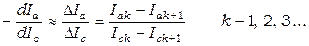, (6.14)
где Iaк, Icк – значения анодного и тока в соленоиде из строки с номером k в таблице 6.1. Значение производной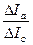 
сопоставляется значению тока в соленоиде из середины интервала 
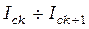(рис. 6.8). 
(6.15)
Пользуясь формулами, продифференцируйте сбросовые характеристики для всех значений на аноде. Результаты вычислений занесите в таблицу 6.2
Таблица 6.2 – Результаты вычислений
| № п/п |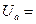 
|
|
| |||
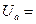
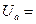
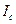 , А
| 
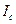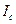| , А
|
| , А
|
| |
 |
2. Постройте график зависимости Iа = Iа (Ic) – сбросовую характеристику. На этом же графике выбрав соответствующий масштаб, изобразите зависимость
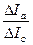от Ic аналогично рис. 6.8.
3. Найдите по таблице 6.2 (или по графику – рис.6.8) максимальное значение производной 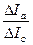. Соответствующий ему ток в соленоиде Ic и будет Iкр. Значения Iкр, определенные для трёх анодных напряжений, занесите в таблицу 6.3.
Таблица 6.3 – Результат эксперимента и погрешности
| Ua =…, Δ Ua = | Ua =…, Δ Ua = | Ua =…, Δ Ua = | |
| Iкр | |||
| ΔIкр | |||
Δ ( )
| |||
| |||
| |||
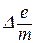
| k ∙Ua | |||
| Δ(k∙Ua) |
4. Вычислите приборный коэффициент k. Для каждого анодного напряжения вычислите произведение kUa и удельный заряд электрона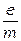 
по формуле (6.12).
Результаты вычислений занесите в таблицу 6.3.
5. Основной вклад в погрешность определения 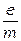дает погрешность определения Iкр связанная в основном с грубостью сетки численного дифференцирования. Поэтому для острого максимума Δ Iкр равно шагу изменения Ic, для широких, искаженных максимумов погрешность увеличивается в два, три раза. Значения Δ Iкр занесите в таблицу 6.3 вместе со значениями 
.
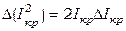6. Вычислите погрешность приборного коэффициента k:
.
Погрешности измерения анодного напряжения Δ Ua, вычислите как приборные по классу точности используемого вольтметра и запишите в таблицу6.3.
7. Вычислите погрешности:
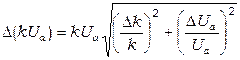(6.16)
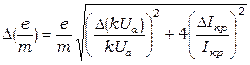(6.17)
Результата вычислений занесите в таблицу 6.3.
8. Вычислите среднее значение 
.
9. Найдите погрешность среднего значения по формуле:
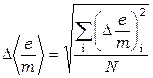,(6.18)
где 
– погрешности отдельных измерений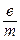 
из таблицы 6.3.
10. Запишите результат в форме 
и сравните его с табличным значением. Сделайте выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется удельным зарядом частицы?
2. Что такое сила Лоренца? Как определить её величину и направление?
3. Рассчитайте параметры траектории заряженной частицы влетающей в однородное магнитное поле перпендикулярно силовым линиям; под углом к силовым линиям.
4. Как будет двигаться частица, если параллельно магнитному полю приложить однородное электрическое поле?
5. Что такое критическая индукция, критический ток?
6. Нарисуйте траектории движения электрона в вакуумном диоде установки при Ic = 0, Ic < Iкр, Ic = Iкр, Ic > Iкр.
7. Что называется сбросовой характеристикой магнетрона? Как объяснить её наблюдаемый вид? Почему при Ic = Iкр анодный ток не превращается в нуль? Как практически определить Iкр.
8. Сформулируйте теорему о циркуляции вектора напряженности магнитного поля (закон полного тока)?
10. Выведите формулу для напряженности (индукции) магнитного поля длинного соленоида.
ЛИТЕРАТУРА [1, с. 219-225], [1, с. 302-309], [3, с. 208-211],
ЛАБОРАТОРНАЯ РАБОТА № 3.7
ИЗМЕРЕНИЕ НАПРЯЖЕННОСТИ ПОСТОЯННОГО МАГНИТНОГО ПОЛЯ
Цель работы: определить горизонтальную составляющую напряженности магнитного поля Земли; измерить напряженность магнитного поля постоянного магнита.
Материалы и оборудование: тангенс-гальванометр, миллиамперметр, однополюсный переключатель, реостат, источник постоянного тока (аккумулятор), короткий цилиндрический постоянный магнит.
Практическое значение: магнитное поле Земли дает возможность ориентироваться относительно стран света и защищает планету от губительного действия высокоэнергетических космических частиц.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Между электрическими токами (движущимися зарядами) обнаруживается специфическое взаимодействие, зависящее от силы токов и их взаимной ориентации, называемое магнитным. Оно осуществляется посредством магнитного поля, которое электрические токи создают в окружающем пространстве. Кроме того, магнитное поле может создаваться постоянными магнитами, переменным электрическим полем, отдельными движущимися зарядами. Подобно тому, как электрическое поле можно исследовать с помощью пробного заряда, магнитное поле может быть исследовано с помощью малого элемента тока длиной D l, малого витка (контура) с током или магнитной стрелки. В соответствии с такими исследованиями в каждой точке магнитного поля может быть задан вектор зависящий только от свойств самого поля. Его модуль может быть определен одним из способов
или 
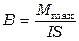(7.1)
где Fmax - максимальная сила, действующая на элемент тока D l, Mmax - максимальный момент сил, действующий на контур с током площадью S, I - сила тока.
Направление вектора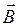 
соответствует направлению тока в элементе D l при котором сила F = 0 или направлению положительной нормали к свободно установившемуся контуру, т.е. при M = 0. Таким образом, магнитное поле является векторным с основной силовой характеристикой вектором 
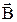, который называется вектором магнитной индукции. Единицей измерения индукции в системе СИ является тесла (Тл = Н / А.м). Используется также вектор напряженности магнитного поля
, (7.2)
где константа m0 = 4p.10-7 Гн/м = 1,256.10-6 Гн/м называется магнитной постоянной; величина m называется магнитной проницаемостью. Она характеризует магнитные свойства среды, в которой исследуется поле (для вакуума m = 1). Магнитное поле графически изображается с помощью силовых линий – плавных линий, касательных к вектору индукции 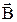или напряженности 
. Силовые линии магнитного поля всегда замкнуты, такие поля называются вихревыми.
Рассматривая электрический ток как совокупность движущихся зарядов, можно получить формулу для расчета магнитного поля элементарного участка проводника длиной dl с током I (закон Био-Савара-Лапласа)
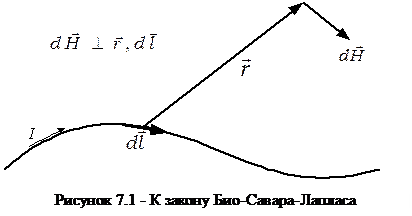
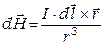, (7.3)
где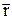 
- радиус-вектор, направленный от элемента провода к точке, в которой определяется напряженность (рис. 7.1), mо - магнитная постоянная. Для определения напряженности магнитного поля провода произвольной формы и длины надо просуммировать векторы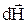 
, создаваемые отдельными элементами dl этого провода, что выражается в форме интеграла
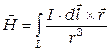, (7.4)
где интегрирование ведется по всей длине L провода. Например, магнитное поле на оси кольцевого проводника с током (рис. 7.2) на расстоянии x от его центра можно получить из (7.4), интегрируя по окружности
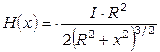. (7.5)
В частности, в центре кольцевого витка (x = 0) поле максимально
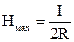. (7.6)
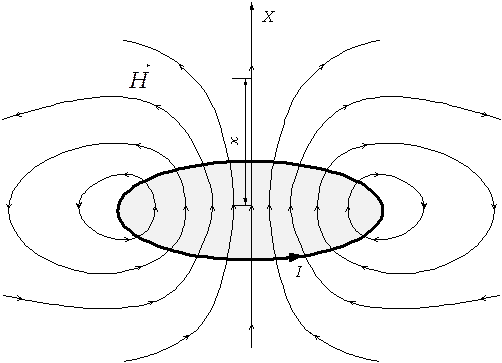
Рисунок 7.2 – Магнитное поле кольцевого тока
Здесь и ниже мы будем опускать значок вектора над H, имея в виду, что речь идет об абсолютной величине напряженности поля. На большом расстоянии от витка (x >> R) на его оси поле убывает пропорционально третьей степени расстояния:
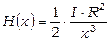. (7.7)
Отметим, что отношение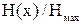 
не зависит от величины тока I
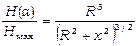. (7.8)
Из формул (7.5) и (7.8) видно, что магнитное поле неоднородно, т.е. существенно зависит от точки наблюдения.
