Розв’язування систем лінійних рівнянь

ЛАБОРАТОРНА РОБОТА №1

Тема: Робота з векторами і матрицями в середовищі MathCAD.

Мета: ознайомитися з системою MathCAD, оволодіти основними навичками праці з системою, навчитися проводити елементарні обчислення з векторами і матрицями. Розглянути методи розв’язання систем лінійних рівнянь.

Питання
Робота з векторами і матрицями в середовищі MathCAD.

1. Розв’язування систем лінійних рівнянь матричним способом.

Теоретичні відомості

Для того, щоб почати роботу з векторами і матрицями в середовищі MathCAD, необхідно на панелі математичних інструментів «Математика» активізувати панель векторних і матричних операцій «Матрицы».

Матриці та вектори

Для створення вектора або матриці у Mathcad достатньо у діалоговому вікні вибрати та задати за допомогою

кількість рядків та стовпчиків. В отриманій матриці заповнюємо місцезаповнювачи необхідними даними

Матриці, вектори та ранжирувані змінні відображаються по-різному в залежності від того, як заданий масив (Рис.1)

Рис.1. Завдання ранжируваної змінної та вектора.

На відміну від звичного позначення членів матриці, коли перший індекс вказує на рядок, а другий на стовпчик і а₁₁, а₁₂ означає, що ми маємо перший елемент у першому стовпчику та перший елемент у другому стовпчику, в Mathcad ці елементи будуть мати індекси а₀₀, а₀₁. Тобто підрахунок ведеться не від 1, а від 0. Між індексами у Mathcad ставимо крапку.

Для виконання будь-якої операції над матрицями достатньо клацнути на відповідну кнопку на панелі інструментів.

В Mathcad з матрицями можна виконувати символьні операції. Меню символьних операцій містить три функції – транспонування, обчислення оберненої матриці та визначника (Рис.2).

Рис. 2.Меню символьних операцій з матрицями.

Для здійснення операцій з використанням меню достатньо виділити матрицю, а потім вибрати потрібний пункт меню клацнувши мишею (Рис.3)

Рис.3.Символьні операції над матрицею.

Крім панелі інструментів для роботи з матрицями призначено спеціальні функції, які можна поділити на групи:

• функції визначення матриць та операції з блоками матриць;
• функції обчислення різних чисельних характеристик матриць;
• функції, що реалізують чисельні алгоритми розв’язування задач;
• функції сортування.

 

 

Розглянемо деякі з них:

1. Функції визначення матриць та операції з блоками матриць.

Ø matrix(m,n,f) – створює та заповнює матрицю А={a_ij}. Що має розмір m´n, кожний елемент якої дорівнює значенню функції f(i,j).

Ø diag(v) – створює діагональну матрицю, елементи головної діагоналі якої зберігаються у векторі v.

 

Ø identity(n) – створює одиничну матрицю порядку n.

2. Функції обчислення різних чисельних характеристик матриць:

Ø last(v) – номер останньої компоненти вектора;

Ø length(v) – кількість компонент вектора;

Ø rows(A) – кількість рядків в матриці;

Ø cols(A) – кількість стовпчиків в матриці;

Ø max(A) – найбільший елемент матриці (вектора);

Ø min(A) – найменший елемент матриці (вектора);

Ø mean(A) – середнє значення матриці (вектора);

Ø ranc(A) – ранг матриці, тощо.

 

 

3. Функції, що реалізують чисельні алгоритми розв’язування задач:

Ø rref(A) – призводить матрицю А до ступінчастого вигляду шляхом елементарних операцій з її рядками;

Ø eigenvals(A) – обчислює власне значення квадратної матриці А;

Ø eigenvecs(A) – обчислює власні вектори квадратної матриці А;

Ø lsolve(A,b) – розв’язує систему лінійних алгебраїчних рівнянь A×x=b, тощо.

4. Функції сортування:

Ø Sort(v) – сортує елементи вектора у порядку зростання їхнього значення;

Ø Reverse(v) – переставляє елементи вектора в оберненому порядку;

Ø Csort(A,n) – переставляє рядки матриці А таким чином, щоб відсортувався n-й стовпчик;

Ø Rsort(A,n) - переставляє стовпчики матриці А таким чином, щоб відсортувався n-й рядок.

Розв’язування систем лінійних рівнянь

1. Розв’язяти систему лінійних рівнянь

Задамо матрицю коефіцієнтів А та вектор правих частин В:

Для знаходження розв’язку системи використовуємо обчислювальну функцію lsolve(A,B)

Можна розв’язати систему використовуючи метод розв’язуючого блоку Given/Find, для цього:

· Задаємо початкові наближення для невідомих (довільні числа);

· Вводимо ключове слово Given;

· Переписуємо систему рівнянь у вигляді логічних рівностей, використовуючи знак 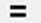, який знаходиться на панелі

· Виводимо результат, використовуючи функцію Find(), причому число аргументів функції Find() повинно бути рівним кількості змінних (Рис.4)

Рис.4. Розв’язок системи рівнянь