Комплексные числа и многочлены
Тема 1 Комплексные числа
Мы надеемся, что вы внимательно ознакомились с введением, и уяснили порядок работы с настоящим пособием.
Начните обязательно с изучения теоретического материала по данной теме. Для этого используйте конспект лекций, рекомендуемые нами учебники или какую-либо другую учебную литературу, которой вы располагаете. Затем, с помощью приведенных ниже вопросов для самоконтроля, проверьте, насколько твердо вы усвоили теорию. Ответы рекомендуем записывать в специальную тетрадь – это впоследствии поможет вам при подготовке к экзамену.
Вопросы для самопроверки
1. Дайте определение комплексного числа, его действительной, мнимой части. Как обозначают действительную и мнимую часть комплексного числа? Какую форму записи комплексного числа называют алгебраической формой?
2. Как геометрически можно изобразить комплексное число? Приведите пример. Какую плоскость называют комплексной плоскостью?
3. Какие числа называют комплексно-сопряженными, противоположными? Как геометрически изображаются эти числа?
4. Какие комплексные числа называются равными? Что означает каждое из утверждений: а) число  равно нулю; б) число
равно нулю; б) число  не равно нулю; в) числа
не равно нулю; в) числа  и
и  различны?
различны?
5. Как выполняются операции сложения, вычитания, умножения, деления комплексных чисел в алгебраической форме? Приведите пример.
6. Дайте определение модуля и аргумента комплексного числа  . Как они обозначаются? Как найти модуль и аргумент?
. Как они обозначаются? Как найти модуль и аргумент?
7. Найдите модули и аргументы чисел, изображенных на рисунке 1.
8.  Как связаны между собой модули и аргументы комплексно сопряженных чисел, противоположных чисел?
Как связаны между собой модули и аргументы комплексно сопряженных чисел, противоположных чисел?
9. Какие формы записи комплексного числа вы знаете? Как осуществляется переход от одной формы к другой? Приведите пример.
10. Как выполняются операции умножения и деления комплексных чисел, заданных в тригонометрической форме? Запишите формулу Муавра.
11. Каков геометрический смысл выражения | z 1 – z 2|?
Если вы сумели ответить на все вопросы, приступайте к выполнению индивидуального задания № 1 (задачи 1- 4).
Если же вам осталось непонятным, как выполнять операции над комплексными числами, то советуем еще раз обратиться к учебнику и конспекту лекций, а затем внимательно разобрать решение предложенных ниже задач. При этом, несомненно, будет полезной и приведенная нами краткая теоретическая информация.
Краткие теоретические сведения
Комплексные числа не являются числами в обычном смысле, они образуют множество С математических объектов, специально построенное таким образом, чтобы выполнялись условия:
I. На множестве С существует квадратный корень из (–1), т.е. существует комплексное число, квадрат которого равен (–1).
II. Множество комплексных чисел С содержит все действительные числа (т.е.  ).
).
III. Арифметические операции: сложение, вычитание, умножение и деление комплексных чисел – определены так, что обладают всеми основными свойствами, какими обладают эти операции на множестве действительных чисел (коммутативность, ассоциативность, дистрибутивность).
1.2.1) Комплексным числом называется упорядоченная пара действительных чисел:  . Комплексное число вида
. Комплексное число вида  отождествляется с действительным числом:
отождествляется с действительным числом:  , в частности,
, в частности,  . Комплексное число
. Комплексное число  обозначается буквой i и называется мнимой единицей:
обозначается буквой i и называется мнимой единицей:  .
.
Два комплексных числа  и
и  равны тогда и только тогда, когда
равны тогда и только тогда, когда  и
и 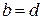 .
.
Сложение, вычитание и умножение комплексных чисел определяются равенствами:
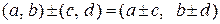 ,
,
 .
.
Из этих определений с очевидностью следуют равенства:
 Þ
Þ  ,
,
 Þ
Þ  .
.
Тогда если  – произвольное комплексное число, то
– произвольное комплексное число, то
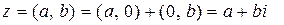 .
.
Поэтому всякое комплексное число  можно записать в виде
можно записать в виде

– это выражение называют алгебраической формой комплексного числа.Число а называют действительной частью комплексного числа  и обозначают
и обозначают  :
:  ; число b называют мнимой частью комплексного числа и обозначают
; число b называют мнимой частью комплексного числа и обозначают  :
: 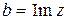 . Число вида
. Число вида  называют чисто мнимым.
называют чисто мнимым.
1.2.2) Сложение, вычитание, умножение комплексных чисел в алгебраической форме выполняется по тем же правилам, что и действия с двучленами, с последующей заменой  на –1:
на –1:
 ,
,
 .
.
Частное от деления числа 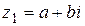 на число
на число  ,
,  , определяется равенством
, определяется равенством

 .
.
Степень 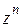 , n ÎN, комплексного числа z определяется равенством
, n ÎN, комплексного числа z определяется равенством

В частности, учитывая i 2 = –1, получаем
 ,
,  ,
,
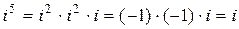 , и т.д.
, и т.д.
В общем случае, для натурального п

 .
.
1.2.3) Комплексное число  называется сопряженным числу
называется сопряженным числу  , а числа z и ` z называют комплексно-сопряженными. Справедливы равенства
, а числа z и ` z называют комплексно-сопряженными. Справедливы равенства
(a + bi) + (a – bi) = a + bi + a – bi = 2 а,
a + bi).(a – bi) = a 2 – (bi)2 = a 2 + b 2,
(a + bi) – (a – bi) = a + bi – a + bi = 2 bi,
следовательно, в результате сложения и умножения комплексно-сопряженных чисел получаются действительные числа, а в результате вычитания – чисто мнимое число.
С помощью понятия сопряженного числа правило деления комплексных чисел можно определить следующим образом

 .
.
Число  называется противоположным числу
называется противоположным числу 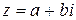 . Очевидно,
. Очевидно,
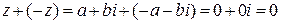 ,
,
 .
.
1.2.4) Комплексное число 
 изображают на координатной плоскости х О у либо точкой М(a; b), либо радиус-вектором
изображают на координатной плоскости х О у либо точкой М(a; b), либо радиус-вектором  этой точки (рисунок 2). Плоскость х О у, на которой изображаются комплексные числа, называют комплексной плоскостью. Ось О х при этом называют действительной осью, т.к. на ней расположены точки, соответствующие действительным числам
этой точки (рисунок 2). Плоскость х О у, на которой изображаются комплексные числа, называют комплексной плоскостью. Ось О х при этом называют действительной осью, т.к. на ней расположены точки, соответствующие действительным числам  . Ось О у называют мнимой осью, на ней лежат точки соответствующие чисто мнимым комплексным числам
. Ось О у называют мнимой осью, на ней лежат точки соответствующие чисто мнимым комплексным числам  .
.
Комплексно-сопряженным числам z и ` z соответствуют точки (векторы), симметричные относительно действительной оси. Противоположные числа z и –z изображаются точками (векторами), симметричными относительно начала координат (рисунок 2).
 В силу геометрического представления комплексного числа в виде вектора, сумму и разность комплексных чисел можно найти графически по правилу сложения векторов (правилу параллелограмма, рисунок 3).
В силу геометрического представления комплексного числа в виде вектора, сумму и разность комплексных чисел можно найти графически по правилу сложения векторов (правилу параллелограмма, рисунок 3).
 Условимся в дальнейшем конкретное (фиксированное) комплексное число обозначать
Условимся в дальнейшем конкретное (фиксированное) комплексное число обозначать  , а произвольное (переменное) комплексное число обозначать
, а произвольное (переменное) комплексное число обозначать  . Числу
. Числу  на комплексной плоскости соответствует переменная (текущая) точка.
на комплексной плоскости соответствует переменная (текущая) точка.
1.2.5) Для комплексного числа  наряду с алгебраической формой записи
наряду с алгебраической формой записи  употребляется и другая, называемая тригонометрической формой:
употребляется и другая, называемая тригонометрической формой:
 .
.
 Здесь
Здесь  – длина вектора
– длина вектора  , изображающего число z (рисунок 4); а j – угол, на который нужно повернуть положительную полуось О х до совмещения ее с вектором
, изображающего число z (рисунок 4); а j – угол, на который нужно повернуть положительную полуось О х до совмещения ее с вектором  .
.
Число r называют модулем комплексного числа z и обозначают  . Модуль любого комплексного числа z определен однозначно: для
. Модуль любого комплексного числа z определен однозначно: для  модуль есть положительное действительное число,
модуль есть положительное действительное число,  ; для
; для  модуль равен нулю,
модуль равен нулю,  .
.
Величину угла j называют аргументом числа z и обозначают  . Если поворот осуществляется против часовой стрелки, то
. Если поворот осуществляется против часовой стрелки, то 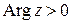 , если – по часовой стрелке, то
, если – по часовой стрелке, то  . Аргумент
. Аргумент  для числа
для числа  определяется не однозначно, а с точностью до слагаемого, кратного 2p. Значение
определяется не однозначно, а с точностью до слагаемого, кратного 2p. Значение  , удовлетворяющее условию
, удовлетворяющее условию  (или
(или  ), называют главным значением аргумента комплексного числа z и обозначают
), называют главным значением аргумента комплексного числа z и обозначают  *). Тогда
*). Тогда 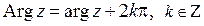 . В дальнейшем будем использовать главное значение аргумента, удовлетворяющее условию
. В дальнейшем будем использовать главное значение аргумента, удовлетворяющее условию  .
.
Для числа  аргумент неопределен, и поэтому можно записать
аргумент неопределен, и поэтому можно записать
 , j – любое.
, j – любое.
Комплексно сопряженные числа  и `
и `  имеют одинаковые модули, а их аргументы отличаются знаком:
имеют одинаковые модули, а их аргументы отличаются знаком:
|  | = | z |, аrg
| = | z |, аrg  = – аrg z (рисунок 5).
= – аrg z (рисунок 5).

Противоположные комплексные числа  и
и  также имеют одинаковые модули, а их аргументы отличаются на
также имеют одинаковые модули, а их аргументы отличаются на 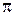 (рисунок 6):
(рисунок 6):
| – z | =| z |, аrg (– z) = p + аrg z.

1.2.6) Действительная часть  , мнимая часть
, мнимая часть  , модуль
, модуль  и аргумент
и аргумент  комплексного числа
комплексного числа  связаны соотношениями
связаны соотношениями
(1)  и (2)
и (2) 
Формулы (1) позволяют от тригонометрической формы комплексного числа  перейти к алгебраической форме
перейти к алгебраической форме 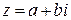 .
.
1.2.7) Переход от алгебраической формы комплексного числа к тригонометрической форме можно осуществить с помощью формул (2) по следующему правилу.
1) Вычислить модуль заданного комплексного числа 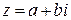 по формуле
по формуле  .
.
2) Найти аргумент*)  числа
числа 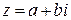 . Для этого:
. Для этого:
а) определить местоположение числа z на комплексной плоскости либо по чертежу, либо в уме;
б) если 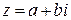 изображается точкой
изображается точкой  , лежащей на одной из координатных осей, то значение
, лежащей на одной из координатных осей, то значение  определяется очевидным образом (рисунок 7).
определяется очевидным образом (рисунок 7).

в) если число 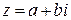 изображаетсяточкой
изображаетсяточкой  (рисунок 8), не лежащей на осях координат, то вычислить
(рисунок 8), не лежащей на осях координат, то вычислить  и найти угол
и найти угол 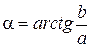 **); затем, учитывая свойство
**); затем, учитывая свойство  , записать:
, записать:
 где
где  .
.

| |||
|


|
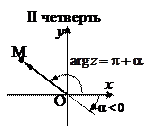
1.2.8) Над комплексными числами, заданными в тригонометрической форме, операции умножения, деления и возведения в целую степень, выполняются по следующим правилам.
А) Чтобы найти произведение двух комплексных чисел, нужно перемножить их модули и сложить аргументы:

Б) Чтобы разделить одно комплексное число на другое, нужно поделить модуль первого на модуль второго, а аргументы – вычесть:
 =
=  ,
,
В) Чтобы возвести комплексное число в целую степень, нужно модуль возвести в эту степень, а аргумент умножить на показатель степени:
 , (
, ( )
)
– эту формулу называют формулой Муавра.
1.2.9) Корнем п -й степени из комплексного числа w называют такое комплексное число z, что 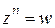 (
( ). Корень п -й степени из числа w обозначается
). Корень п -й степени из числа w обозначается  . Если w ¹ 0, то существует ровно п различных значений
. Если w ¹ 0, то существует ровно п различных значений  .
.
Все значения  корня п -й степени из комплексного числа
корня п -й степени из комплексного числа

можно найти по формуле
 =
=  ,
,
придавая k последовательно значения 0, 1, 2, …, n– 1.
На комплексной плоскости все точки  принадлежат окружности радиуса
принадлежат окружности радиуса 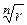 с центром в начале координат. Аргументы соседних точек отличаются друг от друга на
с центром в начале координат. Аргументы соседних точек отличаются друг от друга на  и делят эту окружность на п равных частей. Иными словами, они являются вершинами правильного п -угольника, вписанного в эту окружность.
и делят эту окружность на п равных частей. Иными словами, они являются вершинами правильного п -угольника, вписанного в эту окружность.
Корни п -й степени из числа  , по определению, равны нулю.
, по определению, равны нулю.
В частности, можно доказать, что 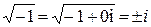 .
.
1.2.10) Комплексное число  может быть записано в показательной форме
может быть записано в показательной форме
 ,
,
где символом  обозначено комплексное число
обозначено комплексное число  .
.
Равенство  =
=  называют формулой Эйлера.
называют формулой Эйлера.
Если даны числа z 1 =  и z 2 =
и z 2 =  , то
, то
 ,
,  ,.
,.
 ,
,  , k = 0, 1
, k = 0, 1  , 2, …, п –1.
, 2, …, п –1.
По определению полагают  .
.
Это значит, что  есть комплексное число, модуль которого равен
есть комплексное число, модуль которого равен  , а аргумент равен b.
, а аргумент равен b.
Для степени  с комплексным показателем сохраняются все свойства, справедливые для степеней с действительным показателем.
с комплексным показателем сохраняются все свойства, справедливые для степеней с действительным показателем.
Перейдем теперь к решению задач
1.3 Примеры решения типовых задач
Пример 1.3.1
Даны числа z 1 = 2 – 3 i, z 2 = – 1 + i. Требуется:
а) аналитически и графически найти z 1 + 2 z 2, z 2 –` z 1;
б) вычислить  ,
,  .
.
Результаты изобразить на комплексной плоскости.
Решение.
а) Числа z1 и z 2 записаны в алгебраической форме, поэтому выполним указанные операции, используя информацию 1.2.2. Получим
z 3 = z 1 + 2 z 2 = (2 – 3 i) + 2(–1 + i) = 2 – 3 i – 2 +2 i = – i;
z 4 = z 2 –` z 1 = (–1 + i) – (2 + 3 i) = –1 + i – 2 – 3 i = –3 – 2 i.
 Выполнить указанные действия графически – это значит, использовать геометрическое представление комплексных чисел
Выполнить указанные действия графически – это значит, использовать геометрическое представление комплексных чисел  и
и  на комплексной плоскости. Число z 1 изображается точкой Z1(2; –3) или вектором
на комплексной плоскости. Число z 1 изображается точкой Z1(2; –3) или вектором  (рисунок 9), а число z 2 – точкой
(рисунок 9), а число z 2 – точкой  или вектором
или вектором  .
.
Тогда числу 2 z 2 соответствует вектор  , а числу
, а числу  – вектор
– вектор  +
+  .
.
Сложение векторов выполним по «правилу параллелограмма» (рисунок 9). В результате получим вектор  =
=  +
+  . Этот вектор есть радиус-вектор точки
. Этот вектор есть радиус-вектор точки  , которая, как следует из рисунка 9, имеет координаты
, которая, как следует из рисунка 9, имеет координаты  . Значит, число
. Значит, число  .
.
Полученный результат совпадает с результатом сложения  , полученным аналитически.
, полученным аналитически.
Найдем графически разность  . Учитывая, что
. Учитывая, что
 ,
,
построим вектор  , соответствующий числу ` z 1 (этот вектор симметричен вектору
, соответствующий числу ` z 1 (этот вектор симметричен вектору  относительно действительной оси, рисунок 10), затем
относительно действительной оси, рисунок 10), затем
построим вектор  , соответствующий числу (–` z 1). Тогда, по «правилу параллелограмма»,
, соответствующий числу (–` z 1). Тогда, по «правилу параллелограмма»,
z 2 –` z 1 = z 2 + (–` z 1) =  +
+ 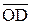 =
= 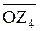 ,
,
а вектор 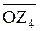 есть радиус-вектор точки
есть радиус-вектор точки  , которая, как следует из рисунка 10, имеет координаты
, которая, как следует из рисунка 10, имеет координаты  . Значит, комплексное число z 4 = –3 –2 i, что также совпадает с результатом, полученным аналитически.
. Значит, комплексное число z 4 = –3 –2 i, что также совпадает с результатом, полученным аналитически.
б) Учитывая правила действий с комплексными числами (информация 1.2.2), находим
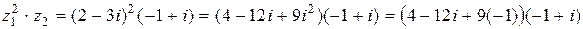 =
=
= 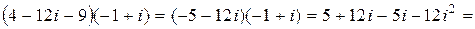
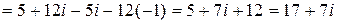 .
.
Полученное комплексное число изображено на рисунке 11 в виде вектора.
Далее находим, используя правило деления комплексных чисел (информация 1.2.3.):
 =
= 
 .
.
Вектор, соответствующий этому числу, изображен на рисунке 12.

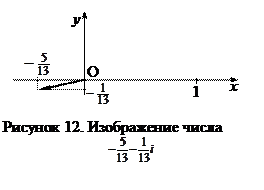
Пример 1.3.2
Найти модули и аргументы заданных комплексных чисел и записать эти числа в тригонометрической форме.
а) z =  ; б) z =
; б) z =  ; в)
; в) 
Решение
а) Число z =  запишем в алгебраической форме:
запишем в алгебраической форме:
 .
.
Тогда его мнимая и действительная части равны соответственно:
 ,
,  .
.
Чтобы найти модуль и аргумент числа, используем информацию 1.2.6. По формуле  находим модуль числа
находим модуль числа  :
:
 .
.
 Аргумент числа найдем, используя изображение этого числа на комплексной плоскости. Числу
Аргумент числа найдем, используя изображение этого числа на комплексной плоскости. Числу  соответствует точка
соответствует точка  , которая расположена на отрицательной части мнимой оси О у (рисунок 13), или вектор
, которая расположена на отрицательной части мнимой оси О у (рисунок 13), или вектор 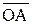 . Поэтому
. Поэтому  .
.
Тогда в тригонометрической форме число  может быть записано следующим образом:
может быть записано следующим образом:
 .
.
Замечание. В рассмотренном случае можно было и модуль числа  найти исходя из геометрического изображения этого числа как длину вектора
найти исходя из геометрического изображения этого числа как длину вектора 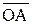 – она, очевидно, равна 3.
– она, очевидно, равна 3.
б) Число z =  также запишем в алгебраической форме:
также запишем в алгебраической форме:
 .
.
Изобразим данное число на комплексной плоскости (рисунок 14) в виде точки  или вектора
или вектора 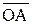 . Из рисунка находим модуль и аргумент числа z =
. Из рисунка находим модуль и аргумент числа z =  :
:

 ;
;
 (или
(или  ).
).
Теперь можно записать заданное число в тригонометрической форме:
 .
.
в) На первый взгляд кажется, что число  записано в показательной форме. Но это не так! Показательная форма
записано в показательной форме. Но это не так! Показательная форма  комплексного числа представляет собой произведение действительного числа
комплексного числа представляет собой произведение действительного числа  и экспоненты
и экспоненты  с чисто мнимым показателем. Поэтому сначала преобразуем заданное число, используя свойства степеней:
с чисто мнимым показателем. Поэтому сначала преобразуем заданное число, используя свойства степеней:

– получили показательную форму записи числа (информация 1.2.10), откуда, очевидно, модуль этого числа равен  , а аргумент
, а аргумент  (рад.).
(рад.).
Теперь, используя формулу Эйлера  =
=  , запишем
, запишем
 .
.
Тогда получим тригонометрическую форму записи заданного числа
 .
.
Пример 1.3.3
Записать заданные комплексные числа в трех формах: алгебраической, тригонометрической, показательной.
а) z =  ; б) z =
; б) z =  .
.
Решение
а) Число z = –  записано в алгебраической форме. Запишем его в тригонометрической форме.
записано в алгебраической форме. Запишем его в тригонометрической форме.
Найдем модуль r и аргумент j числа  , для этого воспользуемся алгоритмом, сформулированным в пункте 1.2 (информация 1.2.6).
, для этого воспользуемся алгоритмом, сформулированным в пункте 1.2 (информация 1.2.6).
1) Действительная и мнимая части данного числа равны соответственно
а =  , b =
, b =  ,
,
поэтому модуль числа равен
 .
.
2) 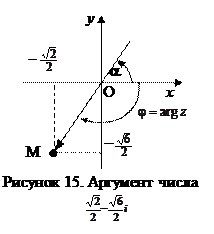 Найдем аргумент числа z = –
Найдем аргумент числа z = –  . Находим:
. Находим:
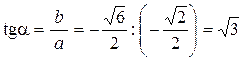 ,
,
откуда 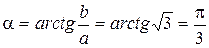 .
.
Точка М  , изображающая заданное число, расположена в III четверти (рисунок 15), поэтому значение
, изображающая заданное число, расположена в III четверти (рисунок 15), поэтому значение  будет равно
будет равно  . Тогда
. Тогда  .
.
3) Запишем тригонометрическую форму числа  :
:
 .
.
Используя найденные значения модуля и аргумента, нетрудно записать число  и в показательной форме:
и в показательной форме:
z = –  =
=  .
.
Таким образом, получено представление комплексного числа z в трех формах:
–  =
=  =
=  .
.
б) Сначала запишем число z =  в алгебраической форме
в алгебраической форме  . Для этого преобразуем
. Для этого преобразуем
 =
=  .
.
Получили алгебраическую форму заданного числа: z =  .
.
Чтобы записать это число в тригонометрической и показательной форме, найдем его модуль r и аргумент j =  . Имеем:
. Имеем:
 ,
,
 .
.
Тогда  .
.
 Так как число
Так как число  изображается точкой
изображается точкой  , принадлежащей II четверти (рисунок 16), то используем формулу
, принадлежащей II четверти (рисунок 16), то используем формулу  , где
, где  (информация 1.2.7). Таким образом,
(информация 1.2.7). Таким образом,
j =  = p + a =
= p + a =  .
.
Так как при решении инженерных задач окончательный результат принято доводить до цифровой десятичной записи числа, то найдем, например, с помощью калькулятора приближенное значение
 (радиан),
(радиан),
отсюда
j =  =
=  = 3,14 – 0,46= 2,68 (радиан).
= 3,14 – 0,46= 2,68 (радиан).
Тогда тригонометрическая форма числа z =  имеет вид
имеет вид
z =  ,
,
а показательная форма z =  .
.
Таким образом, заданное число представлено в трех формах:
 =
=  =
=  =
=  .
.
Пример 1.3.4
Даны комплексные числа z 1 =  и z 2 =
и z 2 =  .
.
Вычислить: а) z 1. z 2; б) z 110; в)  .
.
Решение
а) Чтобы выполнить указанные действия, нужно числа  и
и  записать в одной и той же форме: алгебраической, тригонометрической или показательной. Так как число
записать в одной и той же форме: алгебраической, тригонометрической или показательной. Так как число  легко записать в тригонометрической форме, а степень
легко записать в тригонометрической форме, а степень  проще всего найти с помощью формулы Муавра (информация 1.2.8), то вычисления будем производить, используя тригонометрическую форму комплексных чисел
проще всего найти с помощью формулы Муавра (информация 1.2.8), то вычисления будем производить, используя тригонометрическую форму комплексных чисел  и
и  .
.
Число  =
=  запишем сначала в алгебраической форме, для чего выполним операцию деления числа w 1=
запишем сначала в алгебраической форме, для чего выполним операцию деления числа w 1=  на число w 2 = 1+ i по правилу деления комплексных чисел, записанных в алгебраической форме (информация 1.2.3):
на число w 2 = 1+ i по правилу деления комплексных чисел, записанных в алгебраической форме (информация 1.2.3):
z 1 =  =
= 

 i.
i.
Получили алгебраическую форму числа z 1:
z 1 =  .
.
Найдем тригонометрическую форму этого числа. Имеем

 .
.
 Чтобы найти аргумент числа
Чтобы найти аргумент числа  , можно воспользоваться известным уже алгоритмом (информация 1.2.7, или пример 1.3.3). Но в данном случае аргумент легко определить графически, если изобразить число
, можно воспользоваться известным уже алгоритмом (информация 1.2.7, или пример 1.3.3). Но в данном случае аргумент легко определить графически, если изобразить число  на комплексной плоскости (рисунок 17). Учитывая
на комплексной плоскости (рисунок 17). Учитывая  , видим, что число
, видим, что число  лежит на биссектрисе четвертого координатного угла, значит,
лежит на биссектрисе четвертого координатного угла, значит,
j1 = arg z 1 = 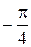 .
.
Тогда тригонометрическая форма комплексного числа  имеет вид
имеет вид
z 1 =  =
=  .
.
Рассмотрим второе число: z 2 =  , его записать в тригонометрической форме совсем просто: для этого достаточно вынести числовой множитель 3 за скобку, а оставшееся в скобках выражение представить в виде суммы
, его записать в тригонометрической форме совсем просто: для этого достаточно вынести числовой множитель 3 за скобку, а оставшееся в скобках выражение представить в виде суммы  , воспользовавшись четностью функции cosj и нечетностью функции sinj:
, воспользовавшись четностью функции cosj и нечетностью функции sinj:
 .
.
Тогда, по правилу умножения комплексных чисел в тригонометрической форме: «модули – перемножить, аргументы – сложить» (информация 1.2.8), получим
z 1. z 2 =  . (
. ( ) =
) =
= 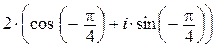 .
.  =
=
=  .
.
Полученное число можно записать в алгебраической форме
z 1. z 2 =  » 1,55 – 5,8 i
» 1,55 – 5,8 i
(значения тригонометрических функций вычислены с помощью калькулятора).
б) Вычислим z 110 =  , используя формулу Муавра (информация 1.2.8) и найденную выше тригонометрическую форму записи числа
, используя формулу Муавра (информация 1.2.8) и найденную выше тригонометрическую форму записи числа  :
:
 =
= 


 .
.
Получили чисто мнимое число –1024 i.
в) Вычислим  . Здесь
. Здесь  – число, сопряженное числу
– число, сопряженное числу
z 1 =  =
= 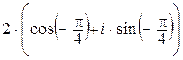
Поскольку комплексно сопряженные числа имеют одинаковые модули, а их аргументы отличаются только знаком (информация 1.2.5), то можно сразу записать число  в тригонометрической форме:
в тригонометрической форме:
 =
=  .
.
Тогда частное от деления  на z 2 =
на z 2 =  найдем по правилу «модули – поделить, аргументы – вычесть» (информация 1.2.8):
найдем по правилу «модули – поделить, аргументы – вычесть» (информация 1.2.8):
 =
= 
=  .
.
Пример 1.3.5
Решить уравнение:
а)  ; б)
; б) 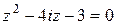 ;
;
в)  ; г)
; г)  .
.
Полученные результаты изобразить на комплексной плоскости.
Решение
а) Решим квадратное уравнение  , используя известный («школьный») алгоритм. Найдем дискриминант
, используя известный («школьный») алгоритм. Найдем дискриминант
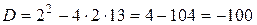 .
.
Если бы требовалось найти действительные корни данного уравнения, то в случае отрицательного дискриминанта мы должны были бы сделать вывод, что действительных корней уравнение не имеет. Но мы ищем решение уравнения на множестве комплексных чисел, где операция извлечения квадратного корня из отрицательного числа определена (информация 1.2.9). Поэтому получаем
 .
.
 Тогда
Тогда 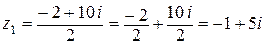 ,
,
 .
.
Итак, корнями данного квадратного уравнения являются комплексные числа  и
и  .
.
Изобразим полученные числа на комплексной плоскости (рисунок 18)
Замечание. Обратите внимание, полученные корни  и
и  являются комплексно сопряженными числами. Можно доказать и в общем случае, что если квадратное уравнение с действительными коэффициентами имеет комплексные корни, то это обязательно комплексно сопряженные числа.
являются комплексно сопряженными числами. Можно доказать и в общем случае, что если квадратное уравнение с действительными коэффициентами имеет комплексные корни, то это обязательно комплексно сопряженные числа.
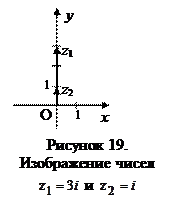 б) Уравнение
б) Уравнение 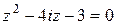 будем решать аналогично предыдущему:
будем решать аналогично предыдущему:
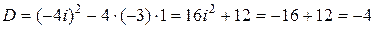 ,
,
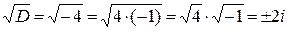 ,
,
 ,
,  .
.
Таким образом, данное квадратное уравнение имеет корни  . Эти корни изображены на рисунке 19.
. Эти корни изображены на рисунке 19.
в) Рассмотрим уравнение  . Как известно, решить уравнение – значит, найти такое число z (вообще говоря, комплексное), которое при подстановке в уравнение обращает его в верное равенство. А найти комплексное число – значит, найти либо его действительную и мнимую части, либо модуль и аргумент.
. Как известно, решить уравнение – значит, найти такое число z (вообще говоря, комплексное), которое при подстановке в уравнение обращает его в верное равенство. А найти комплексное число – значит, найти либо его действительную и мнимую части, либо модуль и аргумент.
Пусть  – искомое число. Тогда | z | =
– искомое число. Тогда | z | =  . Подставив эти выражения в заданное уравнение, получим
. Подставив эти выражения в заданное уравнение, получим
 – (x + iy) – 3 – 2 i = 0.
– (x + iy) – 3 – 2 i = 0.
Запишем обе части этого равенства в виде комплексного числа
( – х – 3) + (– у – 2) i = 0 + 0 i.
– х – 3) + (– у – 2) i = 0 + 0 i.
Учитывая условие равенства комплексных чисел (информация 1.2.2), приравняем соответственно действительные и мнимые части чисел, стоящих в левой и правой частях полученного равенства. Приходим к системе уравнений

Решая второе уравнение системы, находим: у = –2. Преобразуем первое уравнение системы:
 = х +3, (о.д.з. х ³ –3), откуда х 2 + у 2 = (х + 3)2,
= х +3, (о.д.з. х ³ –3), откуда х 2 + у 2 = (х + 3)2,
х 2 + у 2 = х 2 + 6 х + 9, у 2 = 6 х + 9.
Полагая в последнем равенстве у = –2, получим
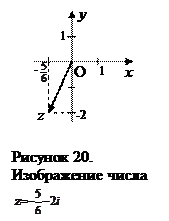 4 = 6 х + 9, 6 х = – 5, х = –
4 = 6 х + 9, 6 х = – 5, х = – 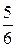 .
.
Итак, найдена действительная  и мнимая
и мнимая 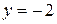 части искомого числа z. Следовательно, решением данного уравнения является число z = –
части искомого числа z. Следовательно, решением данного уравнения является число z = – 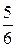 – 2 i. Оно изображено на рисунке 20.
– 2 i. Оно изображено на рисунке 20.
г) Преобразуем заданное уравнение:
 Þ
Þ  Þ
Þ 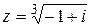 .
.
Следовательно, задача состоит в нахождении всех корней третьей степени из комплексного числа w = –1 + i.
Рекомендуем находить все значения корня  , используя следующий алгоритм.
, используя следующий алгоритм.
1. Записать комплексное число w в тригонометрической форме
 .
.
2. Записать общую формулу корней из данного числа:
 .
.
3. Найти все значения корня по этой формуле, полагая последовательно k = 0, 1, 2, …, n –1.
Используем этот алгоритм для отыскания корней третьей степени из числа  . Запишем это число в тригонометрической форме, для чего находим его модуль и аргумент:
. Запишем это число в тригонометрической форме, для чего находим его модуль и аргумент:
 Þ
Þ  .
.
Тогда  ;
;
 ,
,  ,
,
а так как точка  , изображающая число
, изображающая число  , лежит во второй четверти, то
, лежит во второй четверти, то
j = arg w =  =
=  .
.
Таким образом,  .
.
Тогда значения корня третьей степени из числа w находим по формуле

при k = 0, 1, 2.
Полагая в этой формуле k = 0, получим первый корень заданного уравнения
 .
.
При k = 1 получаем второй корень 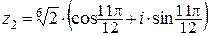 .
.
Наконец, при k = 2 получаем третий корень  .
.
 Геометрически корни
Геометрически корни  заданного уравнения располагаются на окружности радиуса
заданного уравнения располагаются на окружности радиуса 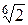 с центром в начале координат и делят ее на три равные части. Корни
с центром в начале координат и делят ее на три равные части. Корни  изображены на рисунке 21, где
изображены на рисунке 21, где 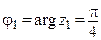 ,
, 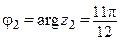 ,
,
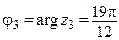 .
.
Пример 1.3.6
Какой геометрический смысл имеет модуль разности 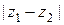 двух комплексных чисел?
двух комплексных чисел?
Решение
Пусть  ,
,  , тогда
, тогда 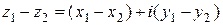 и
и
 =
=  .
.
Из школьного курса геометрии известно, что число  равно расстоянию между точками с координатами
равно расстоянию между точками с координатами  и
и  . Но точки
. Но точки  и
и  на комплексной плоскости соответствуют рассмотренным числам z 1 и z 2.
на комплексной плоскости соответствуют рассмотренным числам z 1 и z 2.
Значит, число






