Порядок виконання. 1.Оцінка керованості і спостережуваності об’єкта, заданого матрицями A, B, C,D

1.Оцінка керованості і спостережуваності об’єкта, заданого матрицями A, B, C,D.

Вводимо вхідні дані, для чого у вікні управління набираємо:

a = [0 0 0 1; -9.7 0 2.2 -7.1; 6.1*exp(-3) 0 -0.12 0.99;0 0 -0.25 -0.96 ];

 

b = [0; 0; 0; -0.5];

 

c = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1];

d = [0];

 

Лінійна стаціонарна система є цілком керованою за станом тоді і тільки тоді, якщо матриця К = [В АВ А²В.. ] має ранг п (де п - кількість рядків матриці А {п х n)) і не є виродженою.

Одержимо матрицю К для об’єкта. Для цього у вікні управління набираємо:

k = ctrb (a, b)

 

k =

0 -0.5000 0.4800 -0.3370

0 3.5500 0.3530 -1.4209

0 -0.4950 0.3827 -0.2338

-0.5000 0.4800 -0.3370 0.2279

 

Перевіримо, чи є матриця К виродженою. Для цього набираємо:

dk = det(k)

 

dk =

-0.0057

 

Ця команда виконується тільки для симетричної матриці.

Знайдемо ранг матриць K Для цього у вікні управління набираємо:

rang_k = rank(k)

 

rang_k =

 

Отримане значення rang_k повинно дорівнювати розмірності матриці А. Лінійна стаціонарна система є цілком спостережуваною тоді і тільки тоді, коли матриця

G = [С^Т C^T (А^Т)²С^Т... має ранг, що дорівнює. кількості рядків матриці А (тобто п), і не є виродженою.

Одержимо матрицю G для системи. Для цього у вікні управління набираємо:

 

S1 = ss(a, b, c, d);,

 

obsv(S1)

 

ans =

1.0000 0 0 0

0 1.0000 0 0

0 0 1.0000 0

0 0 0 1.0000

0 0 0 1.0000

-9.7000 0 2.2000 -7.1000

0.3037 0 -0.1200 0.9900

0 0 -0.2500 -0.9600

0 0 -0.2500 -0.9600

0.6681 0 1.5110 -0.7060

-0.0364 0 -0.2331 -0.7655

-0.0759 0 0.2700 0.6741

-0.0759 0 0.2700 0.6741

0.4589 0 -0.0048 2.8418

-0.0708 0 0.2193 0.4677

0.0820 0 -0.2009 -0.4558

 

g = obsv(a, c)

 

g =

1.0000 0 0 0

0 1.0000 0 0

0 0 1.0000 0

0 0 0 1.0000

0 0 0 1.0000

-9.7000 0 2.2000 -7.1000

0.3037 0 -0.1200 0.9900

0 0 -0.2500 -0.9600

0 0 -0.2500 -0.9600

0.6681 0 1.5110 -0.7060

-0.0364 0 -0.2331 -0.7655

-0.0759 0 0.2700 0.6741

-0.0759 0 0.2700 0.6741

0.4589 0 -0.0048 2.8418

-0.0708 0 0.2193 0.4677

0.0820 0 -0.2009 -0.4558

 

Перевіримо, чи є матриця G виродженою. Для цього набираємо:

dg = det(g)

 

Ця команда виконується тільки для симетричної матриці.

Знайдемо ранг матриць G. Для цього у вікні управління набираємо:

Rahg_g = rank(g)

 

Rahg_g =

 

Отримане значення rang_g повинно дорівнювати розмірності матриці А.

2. Оцінка керованості і спостережуваності об’єкта і незмінної частини системи «об’єкт + сервопривод».

Одержимо передатну функцію системи «об’єкт + сервопривод» з приводом, передатна, функція якого . Для цього у вікні управління набираємо:

 

Wob=tf ([0.5 0.6], [1 1.08 0.3627 0.001525])

 

 

Transfer function:

0.5 s + 0.6

------------------------------------

s^3 + 1.08 s^2 + 0.3627 s + 0.001525

 

 

Wsp1=tf (1, [0.1 1])

 

 

Transfer function:

---------

0.1 s + 1

 

Wraz1= Wob * Wsp1,

 

 

Transfer function:

0.5 s + 0.6

-----------------------------------------------------

0.1 s^4 + 1.108 s^3 + 1.116 s^2 + 0.3629 s + 0.001525

 

 

де Wraz1 - передатна функція системи «об’єкт + сервопривод».

 

Одержимо матриці , , для об’єкта (i=1) і системи «об’єкт + сер­вопривод» (i =2). Для цього у вікні управління набираємо:

[a1, b1, c1, d1]= ssdata(Wob)

 

a1 =

-1.0800 -0.3627 -0.0015

1.0000 0 0

0 1.0000 0

b1 =

c1 =

0 0.5000 0.6000

d1 =

 

[a2, b2, c2, d2]= ssdata(Wraz1)

 

a2 =

-11.0800 -1.3953 -0.0283 -0.0001

8.0000 0 0 0

0 16.0000 0 0

0 0 2.0000 0

b2 =

0.2500

c2 =

0 0 0.1563 0.0937

d2 =

 

 

Одержимо матриці 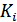для об’єкта (і = 1) і системи «об’єкт + сервопривод» (i = 2). Для цього у вікні управління набираємо:

k1 =ctrb(a1, b1)

 

k1 =

1.0000 -1.0800 0.8037

0 1.0000 -1.0800

0 0 1.0000

 

k2 = ctrb(a2, b2)

 

k2 =

0.2500 -2.7700 27.9009 -279.1287

0 2.0000 -22.1600 223.2074

0 0 32.0000 -354.5600

0 0 0 64.0000

 

Перевіримо, чи є матриці виродженими. Для цього набираємо:

dk1= det (k1)

 

dk1 =

 

dk2= det (k2)

 

dk2 =

 

Знайдемо ранг матриць 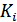Для цього у вікні управління набираємо:

rang_k1=rank(k1)

 

rang_k1 =

 

rang_k2 = rank(k2)

 

rang_k2 =

 

Значення rang_ повинно дорівнювати кількості рядків відповідних матриць .

Одержимо матриці , для об’єкта (і = 1) і системи «об’єкт + сервопривод»(i=2). Для цього у вікні управління набираємо:

g1= obsv (a1, c1)

 

g1 =

0 0.5000 0.6000

0.5000 0.6000 0

0.0600 -0.1814 -0.0008

 

g2 =obsv(a2, c2)

 

g2 =

0 0 0.1563 0.0937

0 2.5000 0.1875 0

20.0000 3.0000 0 0

-197.6000 -27.9068 -0.5670 -0.0012

 

Перевіримо, чи є матриці виродженими. Для цього набираємо:

dg1=det (g1)

 

dg1 =

-0.0758

 

dg2=det (g2)

 

dg2 =

-3.2576

 

 

Знайдемо ранг матриць . Для цього у вікні управління набираємо:

rang_g1 = rank(g1)

 

rang_g1 =

 

 

rang_g2 = rank(g2)

 

rang_g2 =

 

 

Значення rang_ 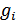повинні дорівнювати розмірності відповідних матриць .

3.Пункт 2 виконати з передатною функцією