ЛАБОРАТОРНА РОБОТА 1
Дослідження стійкості об’єкта
Мета роботи - дослідження стійкості об’єкта, математичну модель якого задано рівняннями простору станів.
Дано
Модель системи у формі простору станів задано матрицями
A= 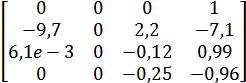 , B =
, B = 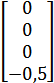 , C =
, C =  , D = [0].
, D = [0].
Необхідно одержати
Передатні функції, корені характеристичного полінома, реакцію системи на одиничний східчастий вплив.
Порядок виконання
1. Вводимо вхідні дані. Для цього у вікні управління MATLAB набираємо:
A = [ 0 0 0 1; -9.7 0 2.2 -7.1; 6.1*exp(-3) 0 -0.12 0.99;0 0 -0.25 -0.96 ];
B = [0; 0; 0; -0.5];
C = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1];
D = [0];
SYS = ss(A, B, C, D),
a =
x1 x2 x3 x4
x1 0 0 0 1
x2 -9.7 0 2.2 -7.1
x3 0.3037 0 -0.12 0.99
x4 0 0 -0.25 -0.96
b =
u1
x1 0
x2 0
x3 0
x4 -0.5
c =
x1 x2 x3 x4
y1 1 0 0 0
y2 0 1 0 0
y3 0 0 1 0
y4 0 0 0 1
d =
u1
y1 0
y2 0
y3 0
y4 0
Continuous-time model.
де sys - ім’я моделі.
2.Представимо модель у формі передатних функцій. Для цього у вікні управління набираємо:
W=tf (SYS).
Transfer function from input to output...
-0.5 s - 0.06
#1: -----------------------------------
s^3 + 1.08 s^2 + 0.3627 s + 0.07593
3.55 s^2 + 4.187 s + 0.2479
#2: ---------------------------------------
s^4 + 1.08 s^3 + 0.3627 s^2 + 0.07593 s
-0.495 s - 0.1519
#3: -----------------------------------
s^3 + 1.08 s^2 + 0.3627 s + 0.07593
-0.5 s^2 - 0.06 s
#4: -----------------------------------
s^3 + 1.08 s^2 + 0.3627 s + 0.07593
У результаті одержуємо передатні функції від кожного входу по кожному виходу.
3.Знайдемо корені характеристичного полінома.
а)Для цього у вікні управління набираємо:
pole (SYS).
ans =
-0.1781 + 0.2705i
-0.1781 - 0.2705i
-0.7238
Определение временных и частотных характеристик систем автоматического управления в Matlab
Цель работы: получение навыков исследования линейных динамических моделей в программном пакете Matlab и ознакомление с временными и частотными характеристиками систем автоматического управления (САУ).
1. Создадим LTI-объект с именем W:
>> W=tf ([-.5 -0.06], [1 1.08 0.3627 0.001525])
Transfer function:
-0.5 s - 0.06
------------------------------------
s^3 + 1.08 s^2 + 0.3627 s + 0.001525
2. Найдем полюса и нули передаточной функции с использованием команд pole, zero.
>> pole(W)
ans =
-0.5379 + 0.2623i
-0.5379 - 0.2623i
-0.0043
>> zero(W)
ans =
-0.1200
3. Построим переходную функцию командой step(W).
>>step(W)
step(W,12),grid,title('W')
линейная модель matlab команда
4. Построим импульсную переходную функцию командой impulse(w).
>> impulse(W)
5. Диаграмму Боде получим, используя команду bode(W)
>>bode(W)
6. Определим частотный годограф Найквиста, выполнив команду nyquist(w)
>> nyquist(W)
Знайдемо корені характеристичного полінома с использованием команды solve
n=solve('s^3 + 1.08*s^2 + 0.3627*s + 0.001525=0')
n =
[ -.53787082010075255328590205528788-.26232439065009344961818894504406*i]
[ -.53787082010075255328590205528788+.26232439065009344961818894504406*i]
[ -.42583597984948934281958894242347e-2]
s=solve('s^4 + 1.08*s^3 + 0.3627*s^2 + 0.0001525*s=0')
s =
[ 0]
[ -.53978950739976351444531001809595-.26621946005720329112758771583220*i]
[ -.53978950739976351444531001809595+.26621946005720329112758771583220*i]
[ -.42098520047297110937996380809810e-3]
m=('s^4 + 1.08*s^3 + 0.3627*s^2 + 0.0001525*s=0')
m =
s^4 + 1.08*s^3 + 0.3627*s^2 + 0.0001525*s=0
p=solve(m)
p =
[ 0]
[ -.53978950739976351444531001809595-.26621946005720329112758771583220*i]
[ -.53978950739976351444531001809595+.26621946005720329112758771583220*i]
[ -.42098520047297110937996380809810e-3]
У результаті одержуємо колонку, що містить визначені корені:
-0,0043
-0,5379 + 0,2623/
-0,5379-0,2623/
б)Корені характеристичного полінома можна знайти, використовуючи команду
damp ('sys').
Eigenvalue Damping Freq. (rad/s)
-5.26e-001 + 8.50e-001i 5.26e-001 1.00e+000
-5.26e-001 - 8.50e-001i 5.26e-001 1.00e+000
Якщо ввести її у вікні управління, то після виконання одержимо три стовпчики з цифрами. Перший (Eigenvalue) містить власні значення або корені характеристичного полінома, другий {Damping) - коефіцієнти демпфірування, третій (Freq. (rad/s)) - власні частоти (рад/с).
4.Побудуємо реакцію системи на одиничний східчастий вплив. Для цього у вікні управління набираємо:
step (SYS).
У результаті виконання цієї команди з’явиться вікно з перехідним процесом
.step (SYS)






