Скорость горения пороха (процесс распространения химической реакции
в глубь зерна) в основном зависит от природы и его начальной температуры, а так же от давления и температуры окружающих его газов.
в орудии и от скорости течения газов (эрозионное горение).
Функциональная зависимость скорости горения - U от давления вида
U= f(p) носит название " закона скорости горения ". Различные авторы дают различные эмпирические формулы для этого закона. Это связано от условий экспериментов и, в первую очередь, от диапазона давлений, в котором проводились опыты и обрабатывались результаты экспериментов. Наиболее употребительные следующие формулы:
а) Формула Вьеля (степенной закон)
(5.1)
A и 
константы, зависящие от природы пороха.
б) Двухчленная формула (линейный закон)
(5.2)
a и b - константы, зависящие от природы пороха.
в) Формула Шарбонье (пропорциональный закон)
(5.3),
где U1 - коэффициент пропорциональности, зависит от природы пороха.
В случае использования степенного закона горения пороха Вьель получил для дымных порохов =0,5, для бездымных порохов = 2/3, для медленно горящих дымных порохов (в дистанционных трубках) =0,2.
Г.А. Забудский для нитроглицериновых порохов принимал = 0,93.
Некоторые авторы для кордитов принимают =1 и для баллиститов =1,07. Степенной закон наиболее точно описывает скорость горения в диапазоне малых давлений (от 0 до 400 кг/см2). Двухчленная формула, применённая впервые профессором С.П. Вуколовым, а, затем И.П. Граве и, значительно позже Мюрауром, позволяет описывать закон горения при давлении p>400 кг/см2. Как показал И.П. Граве обе формулы одинаково пригодны (степенной закон и линейный закон) при давлениях более 400 кг/см2 (см. рис.24 фиг.38).
При решении основной задачи внутренней баллистики Н.Ф. Дроздов использовал формулу Шарбонье.В 1913г Шмиц, сжигая трубчатый порох в большой бомбе Крунна(W0=3.5 дм3) и применив для регистрации давления оптический метод записи упругих деформаций, получил полную кривую записи нарастания давления и на опыте доказал справедливость закона скорости горения в виде:
Если справедлив этот закон и так как скорость горения есть 
где de-преращение сгоревшего слоя за время dt то;
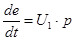
или 
Интегрируя получим 
или 
откуда 
Величины "e1" и "U1" характеризуют размеры и природу пороха и независит от условий заряжания. Проведя опыты по сжиганию одного и того же пороха трубчатой формы в бомбе Крунна при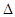 
от 0.12 кг/дм3 до 0.26 кг/дм3 и измерив площадь кривых давлений p(t), Шмиц нашел,что действительно 
найденные из опытов равны между собой. На рис.25 (фиг.39) показаны вид и расположение кривых p(t). В дальнейшем этот закон подтвердили Мюраур, М.Е. Серебряков и др.
Размерность U1 видна из равенства U1= 
.
Величина U1 является, как сила пороха f и коволюм 
- основной баллистической характеристикой пороха и зависит так же как f и от физико-химической природы пороха. Величина U1 для нитроглицериновых порохов 
.
Озависимости U1 от ряда факторов упоминалось ранее.
Шмиц проводил свои опыты при 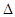от 0,12 до 0,26. Более поздние опыты показали, что при очень... плотность их заряжания (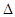 
0,015 кг/дм3)
интеграл является линейной убывающей функцией от времени
.
В опытах М.Е. Серебрякова и А.И. Кохонова было показано, что изменяется с увеличением времени горения только для порохов, имеющих значительную толщину (2е1>0,5); для очень тонких, быстро сгорающих порохов полный импульс даже при малых плотностях заряжания не зависит от 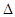. Это указывает на то, что здесь играет скорость процесса,от которого зависит прогревание пороховой массы в слое, непосредственно прилегающем к горящей поверхности S, от повышения температуры увеличивается скорость горения U1 и уменьшается интеграл .
Убывание Ik с уменьшением 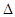для таких порохов при 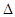<0.1 кг/дм3 является так же следствием прогревания пороховой массы при относительно медленном сгорании, причем это прогревание тем больше, чем медленнее горит порох, т.е. меньше 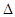. В этом случае наиболее целесообразно использовать степенной закон. В опытах М.Е. Серебрякова (1932 г.) с порохом на твердом растворителе при давлении Рm<1000 кг/см2 можно принять 
. Поскольку в орудиях пороха горят при высоких давлениях и при больших 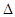, то для них можно считать справедливым скорость горения .
Этот закон справедлив для давлений до 20000 кг/см2. На что указывают опыты французских исследователей.
О влиянии 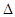и геометрических размеров при больших 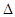>0,6 кг/дм3 свидетельствуют опыты, проведенные Ю.Ф. Христенко в монометрических бомбах его собственных конструкций (описание их дано в главе 3.1.). 
Была проведена серия экспериментов на модернизированной диафрагменной бомбе, где давление сбрасывалось в течении 0.1-0.2 мсек., почти мгновенно.
Эксперименты проводились для одноканального пороха **ВТМ при плотностях заряжания 
и 
**вставка
На рис. (фиг.7)представлены экспериментальные данные с порохом ВТМ в монометрической бомбе с диафрагмой для плотности заряжания 
и 
.Можно отметить большой разброс по давлению от опыта к опыту при . При обработке этих данных необходимо изменять коэффициент U1 с 
до 
начиная с 
для согласования расчетных и опытных данных. Коэффицентами согласования являются также 
и 
.
