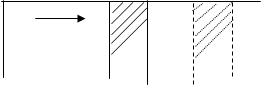
Определим внешнюю работу для случая, показанного на рис. 6. В цилиндре площадью сечение F помещен газ под давлением р. Цилиндр имеет дно и подвижный поршень, который удерживается противодавлением, а также давлением при нагревании газа весом 1 кг, помещенного между дном цилиндра и поршнем. Поршень будет (без трения) перемещаться вдоль цилиндра, испытывая противодавление р.
 |
p p
 | |||||
 | |||||
 | |||||
ds
Рис. 6
Считается, что процесс перемещения поршня таков, что газ находится в равновесном состоянии, т.е. процесс равновесный, тогда работа за время перемещения цилиндра на расстояние ds будет равна
dℓ = p·F·ds = p·dw
где: р·F – сила;
ds – расстояние.
Для конечного пути перемещения поршня внешняя работа будет равна (см. рис. 7)
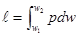
Для изобарного процесса (р = const)
ℓр = p (w2 – w1)
Для изохорного процесса (w = const) w2 = w1
ℓw = p · 0 = 0
р
р1 A
 | ||
 |
р2 В
 |
w1 w2 w
Рис. 7
Для других процессов (рис.7) работа показана как заштрихованная площадь фигуры w1AВw2.
Ясно, что внешняя работа зависит от характера процесса. Для произвольного количества газа она равна
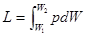(2.18.)
