Можно показать, что для контура, изображённого на рис. 1,
Q = 
= 
, (9)
R П = r + R + R L,
где R П – полное сопротивление цепи; r – внутреннее сопротивление источника тока; R – сопротивление резистора, включенного в контур; R L – активное сопротивление катушки индуктивности.
1. Расчет теоретического значения добротности Q ТЕОР
Добротность контура Q ТЕОР можно рассчитать по формуле (9), зная параметры электрической цепи R П, L и C.
2. Определение добротности по измерениям резонансного напряжения U 0 РЕЗ и амплитуды вынуждающей э. д. с. E0
Соотношение (8) при малых коэффициентах затухания принимает вид
U 0 РЕЗ = 
= E 0 Q,
откуда
Q =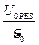 
. (10)
3. Определение добротности по ширине резонансной кривой
Шириной резонансной кривой называется разность частот W1 и W2, при которых достигается эффективное значение резонансного напряжения на конденсаторе, равное (см. рис. 3) U 0 = 
.
Разность этих частот DW = W2 - W1 называется полосой пропускания контура.
Энергия, запасенная в контуре при резонансе, на границах полосы пропускания уменьшается в два раза.
Пользуясь соотношениями (9) и (10) и преобразуя уравнение (5), получаем, что с достаточной степенью точности
Q»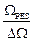 
. (11)
Таким образом, зная DW и WРЕЗ, можно вычислить добротность контура.
Расчет добротности этим методом производится с помощью полученной экспериментально резонансной кривой, построенной в координатах U 0 , W: определяются значения W1 и W2, соответствующие напряжению U 0 = » 0,7 U 0 слева и справа от максимума, после чего вычисляется их разность DW = W2 - W1.
В данной работе циклическим частотам WРЕЗ, W1 и W2 соответствуют значения частоты генератора f = W/(2p) [Гц], поэтому
Q =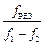 
. (12)
