Метод Гаусса является наиболее распространённым методом решения систем линейных уравнений как вида (1), так и произвольных систем m линейных уравнений c n неизвестными.
Метод Гаусса - это метод последовательного исключения неизвестных. Исключение неизвестных осуществляется при помощи следующих преобразований системы:
· умножения уравнения системы на число, отличное от нуля;
· перестановки местами двух уравнений системы;
· прибавления к одному уравнению системы другого, умноженного на какое-либо число.
Процесс исключения неизвестных состоит в переводе исходной системы линейных уравнений в такую равносильную систему, в которой каждое следующее уравнение содержит по крайней мере одним неизвестным меньше, чем предыдущее. Если этот процесс завершён, то решение системы находится следующим образом: из последнего уравнения определяется одно из неизвестных, затем подстановкой в предыдущее уравнение определяется другое неизвестное, далее вновь подстановкой в предшествующее уравнение находится ещё одно неизвестное и т.д., пока не определяются все неизвестные.
Процесс последовательного исключения неизвестных может быть реализован различными вычислительными схемами, например, схемой с выбором главного элемента в столбце. Суть её заключается в следующем.
Рассмотрим систему (1). Выберем среди коэффициентов а11 , а21,..., аn1 при неизвестном х1 наибольший по абсолютной величине. Уравнение с выбранным наибольшим коэффициентом при х1 поставим первым в системе (1). Пусть наибольшим по абсолютной величине будет коэффициент а11. Разделим обе части первого уравнения на а11, получим уравнение вида
 , (5)
, (5)
где  .
.
С помощью уравнения (5) исключим во всех уравнениях системы (1), начиная со второго, слагаемые, содержащие х1. Для этого умножим обе части уравнения (5) последовательно на а21 , а31 ,..., аn1 и вычтем соответственно из 2-го, 3-го,..., n -го уравнений системы (1).
В результате получим систему (n - 1)-го порядка вида
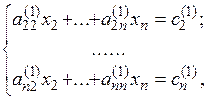 (6)
(6)
где 
Аналогично преобразуем систему (6). Выберем среди коэффициентов  при неизвестном х2 наибольший по абсолютной величине. Пусть наибольшим будет коэффициент
при неизвестном х2 наибольший по абсолютной величине. Пусть наибольшим будет коэффициент  . Уравнение с этим коэффициентом при х2 поставим первым в системе (6) и т.д. После n таких шагов получим систему с треугольной матрицей вида
. Уравнение с этим коэффициентом при х2 поставим первым в системе (6) и т.д. После n таких шагов получим систему с треугольной матрицей вида
 (7)
(7)
эквивалентную системе (1).
Преобразование системы (1) в равносильную систему (7) называется прямым ходом метода Гаусса.
Нахождение переменных из системы (7) называется обратным ходом. Действительно, из последнего уравнения найдём хn, подставим его в предпоследнее уравнение, найдём хn-1 и т.д. Подставив в первое уравнение найденные хn, хn-1,..., х2, получим х1.
Мы рассмотрели идею метода Гаусса (схема с выбором главного элемента в столбце) на примере вычисления системы линейных уравнений вида (1). Если рассматривать общий случай – решение системы, в которой число уравнений не равно числу неизвестных, то в конце преобразований можем получить систему не с треугольной матрицей (7), а ступенчатую.
Коэффициенты  называются главными (ведущими) элементами метода Гаусса.
называются главными (ведущими) элементами метода Гаусса.
Обычно все вычисления при использовании метода Гаусса заносят в таблицу. Для проверки правильности нахождения промежуточных и конечных результатов в таблицу включают столбец контрольных сумм å. Над контрольными суммами (как при прямом, так и при обратном ходе) производятся те же действия, что и над элементами матрицы. Если в вычислениях не будет ошибок, то контрольная сумма å в каждой строке будет совпадать с суммой элементов данной строки S.
Для системы линейных уравнений 3-го порядка

таблица выглядит следующим образом.
| Коэффициенты при неизвестных х 1 х 2 х 3 | Свободный член | Контрольная сумма å | Разность К = å - S | ||
| а 11 а 21 а 31 | а 12 а 22 а 32 | а 13 а 23 а 33 | с 1 = а 14 с 2 = а 24 с 3 = а 34 |   
| |
c 12 = 
| c 13 = 
| c 14 = 
| c 15 = 
| К 1 | |
 = а 22 - а 21 c 12 = а 22 - а 21 c 12
 = а 32- а 31 c 12 = а 32- а 31 c 12
|  = а 23- а 21 c 13 = а 23- а 21 c 13
 = а 33- а 31 c 13 = а 33- а 31 c 13
|  = а 24- а 21 c 14 = а 24- а 21 c 14
 = а 34- а 31 c 14 = а 34- а 31 c 14
|  = а 25 - а 21 c 15 = а 25 - а 21 c 15
 = а 35 - а 31 c 15 = а 35 - а 31 c 15
| К 2 К 3 | |
 = =  
|  = = 
|  = = 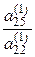
| К 4 | ||

| 
| 
| К 5 | ||
 = = 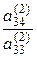
|  = = 
| К 6 | |||
х 3 = 
| 
| К 7 | |||
х 2=
= 
| 
| К 8 | |||

| 
| К 9 |
К 1 = c 15 - (1 + 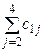 ), К 2 =
), К 2 =  -
-  , К 3 =
, К 3 = 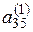 -
-  ,
,
К 4 = 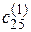 - (
- ( ), К 5 =
), К 5 = 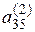 - (
- ( ), К 6 =
), К 6 =  - (
- ( ),
),
К 7 =  , К 8 =
, К 8 =  , К 9 =
, К 9 =  .
.
Пример. Решите систему уравнений методом Гаусса по схеме с выбором главного элемента в столбце

с точностью до 10-2.
Решение. Вычисления, проведённые с помощью табличного процессора Excel, занесём в таблицу.
| Коэффициенты при неизвестных х 1 х 2 х 3 | Свободный член | Контрольная сумма å | Разность Кi = å - S i | ||
| 3,10 | -1,9 | -1,2 | 1,1 | 1,10 | |
| 1,2 | 3,1 | -0,5 | 1,7 | 5,5 | |
| -0,3 | -0,5 | 0,7 | 0,8 | 0,7 | |
| -0,6129 | -0,3871 | 0,3548 | 0,2258 | -0,1290 | |
| 3,8355 | -0,0355 | 1,2742 | 5,2290 | 0,1548 | |
| -0,6839 | 0,5839 | 0,9065 | 0,7677 | -0,0387 | |
| -0,0093 | 0,3322 | 1,3633 | 0,0404 | ||
| 0,5775 | 1,1336 | 1,7001 | -0,0111 | ||
| 1,9629 | 2,9436 | -0,0192 | |||
| 1,9629 | 2,9436 | -0,0192 | |||
| 0,3504 | 1,3906 | 0,0402 | |||
| 1,3294 | 2,2176 | -0,1118 |
Получим решение заданной системы уравнений:
х = 1,3294; у = 0,3504; z = 1,9629.
С точностью до сотых получим ответ:
х» 1,33; у» 0,35; z» 1,96.
Видим, что вычисление по данной схеме «вручную» является довольно трудоёмким занятием, которое можно облегчить, применяя компьютер. Однако этот процесс можно значительно упростить, если преобразования Гаусса проводить не с самими уравнениями системы, а с матрицей их коэффициентов.
Рассмотрим систему m линейных уравнений c n неизвестными. Если к основной матрице А системы прибавить вектор-столбец свободных коэффициентов, то получим расширенную матрицу системы:
 .
.
Иногда в расширенной матрице столбец свободных членов отделяют от других элементов пунктирной чертой.
Преобразованиям систем линейных уравнений отвечают следующие элементарные преобразования матриц:
· умножение строки на число, отличное от нуля;
· перестановка местами двух строк;
· прибавление к одной строке другой, умноженной на какое-либо число.
Две матрицы, приводящиеся одна к другой при помощи конечного числа элементарных преобразований, называются эквивалентными. Очевидно, что эквивалентным матрицам отвечают равносильные системы уравнений.
Таким образом, суть метода Гаусса состоит в преобразовании исходной расширенной матрицы к матрице ступенчатого (или треугольного) вида (прямой ход), из которой затем последовательно (обратным ходом) получаются значения всех неизвестных.
При этом возможны три случая:
1) система несовместна, если в процессе преобразований получено противоречивое равенство (строка расширенной матрицы вида: 0 0 0 … 0  );
);
2) система имеет единственное решение, если основная матрица системы приведена к треугольному виду;
3) система имеет бесконечное множество решений, если основная матрица системы приведена к ступенчатому виду.
Пример. Решите систему уравнений методом Гаусса

Решение. Для данной системы запишем соответствующую расширенную матрицу и с помощью элементарных преобразований
приведём её к ступенчатому виду:

 .
.
Здесь мы применили следующие элементарные преобразования:
1) переставили местами 4-ю и 1-ю строки;
2) последовательно ко 2-й, 3-й и 4-й строкам прибавили первую строку, умноженную соответственно на (- 1), (- 3), (- 2); тем самым в 1-м столбце получили все нули, кроме первого элемента;
3) последовательно к 3-й и 4-й строкам прибавили вторую строку, умноженную соответственно на (- 4) и (- 5); тем самым во 2-м столбце получили нули, кроме первых двух;
4) из 4-й строки вычли 3-ю, получили нулевую строку;
5) удалили нулевую строку.
В результате расширенную матрицу размера 4  4 привели к ступенчатому виду (матрице размера 3
4 привели к ступенчатому виду (матрице размера 3  4), при этом основная матрица приведена к треугольному виду.
4), при этом основная матрица приведена к треугольному виду.
Полученная ступенчатая матрица равносильна системе уравнений:

Из последнего уравнения z = - 4. Подставив z = - 4 во второе
уравнение, получим y = - 2. Подставив z = - 4 и y = - 2 в первое уравнение, получим x = - 1. Итак, система имеет единственное решение: x = - 1; y = - 2; z = - 4.
Пример. Решите систему уравнений методом Гаусса

Решение. Для данной системы запишем соответствующую расширенную матрицу и с помощью элементарных преобразований
приведём её к ступенчатому виду:
 .
.
Здесь мы применили следующие элементарные преобразования:
1) последовательно ко 2-й и 3-й строкам прибавили первую строку, умноженную соответственно на (- 1), (- 3);
2) к 3-й строке прибавили вторую строку, умноженную на (- 2). При этом получили противоречивое равенство:
0· х + 0· у + 0· z = -1,
следовательно, система уравнений несовместна.






