Способом

Рассмотрим систему n линейных уравнений c n неизвестными:

(1)

Это частный случай СЛУ, в которой число уравнений m равно числу неизвестных n. Заметим, что только при выполнении этого условия применим матричный метод.

По правилу умножения матриц систему (1) можно записать в виде матричного уравнения

А×Х = С, (2)

где А - заданная матрица (основная матрица системы);

С - заданный вектор-столбец свободных коэффициентов;

Х - неизвестный вектор-столбец.

Решением матричного уравнения (2) является такой вектор-столбец Х, который обращает уравнение (2) в тождество.

Воспользуемся обратной матрицей для решения матричного уравнения (2), а следовательно, и системы линейных уравнений (1).

Умножим уравнение (2) слева на А ^-1, получим:

А ^-1×А ×Х = А ^-1×С Þ

Е ×Х = А ^-1×С Þ

Х = А ^-1×С. (3)

Таким образом, (3) - решение уравнения (2), так как, подставив (3) в (2), получим верное тождество:

А ×(А ^-1× С) = С Þ

А ×А ^-1× С = С Þ

Е ×С = С Þ С = С.

Поскольку обратную матрицу можно найти только при условии, что det A = D ¹ 0, то и сам матричный способ решения системы линейных уравнений можно применять при выполнении этого условия.

Пример. Решите систему уравнений матричным способом:

Решение. 1) Введём обозначения:

А = ; С = .

2) Вычислим det A = D = 10.

3) Найдём обратную матрицу А^-1.

Для этого сначала вычислим алгебраические дополнения всех элементов матрицы А:

А₁₁ = = - 11; А₁₂ = - 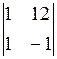=13; А₁₃ = = 2;

 

А₂₁ = - = 5; А₂₂ = = - 5; А₂₃ = - = 0;

 

А₃₁ = 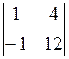= 16; А₃₂ = - = - 8; А₃₃ = = - 2.

Запишем новую матрицу, составленную из алгебраических дополнений:

= .

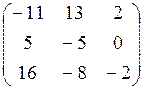Транспонируем матрицу :

^Т= .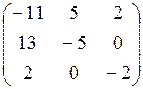

Получим обратную матрицу А^-1:

А^-1= ^Т .

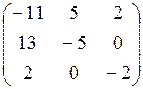
4) Найдём решение системы уравнений в виде вектор-столбца:

Х = А ^-1×С = × = .

Таким образом, решением заданной системы уравнений являются следующие значения:

x = 0.8; у = - 0.4; z = 0.4.