Введение вектора: 
во многих случаях значительно упрощает изучение поля в диэлектриках.
Соотношения (2.11) и (2.12) справедливы для любого диэлектрика, как изотропного, так и анизотропного. Как видно из выражения (2.11), размерность вектора та же, что и вектора 
. Единицей величины служит кулон на квадратный метр (Кл/м2).
В случае изотропных диэлектриков поляризованность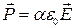 
. Подставив это соотношение в (2.12), получим
(2.13)
где ε — диэлектрическая проницаемость вещества. Диэлектрическая проницаемость ε (как и α) является основной электрической характеристикой диэлектрика. Для всех веществ ε > 1, для вакуума ε = 1. Значения ε зависят от природы диэлектрика и колеблются от величин; весьма мало отличающихся от единицы (газы) до нескольких тысяч (у некоторых керамик). Большое значение ε имеет вода (ε = 81).
Из формулы (2.13) видно, что в изотропных диэлектриках вектор D коллинеарен вектору Е. В анизотропных же диэлектриках эти векторы, вообще говоря, не коллинеарны.
Методические указания
Обычно в задачах курса общей физики рассматривают лишь диэлектрики, которые удовлетворяют следующим условиям: они изотропны и однородны; имеют форму, при которой ограничивающие их поверхности совпадают с эквипотенциальными поверхностями внешнего поля. Сюда относятся диэлектрики в плоских, цилиндрических и сферических конденсаторах. В этих случаях расчет поля в диэлектрике проводится по теореме Гаусса для вектора (2.11), а выражения для векторов , 
рассчитывается по формулам (2.6) и (2.13).
Пример 2.1. Точечный сторонний заряд q находится в центре сферического слоя неоднородного изотропного диэлектрика, проницаемость которого изменяется только в радиальном направлении по закону ε = α/r, где α — постоянная, r — расстояние от центра системы. Найти объемную плотность ρ ' связанных зарядов как функцию r внутри слоя.
Решение. Воспользуемся уравнением (2.7), взяв в качестве замкнутой поверхности сферу радиусом r, центр которой совпадает с центром системы. Тогда
где q'(r) — связанный заряд внутри этой сферы. Запишем дифференциал этого выражения:
где dq' — связанный заряд в тонком слое между сферами радиусов r и r + dr. так как dq' = 
преобразуем к виду
откуда
В нашем случае
После преобразований получаем
Пример 2.2. Сторонние заряды равномерно распределены с объемной плотностью ρ > 0 по шару радиусом а из однородного диэлектрика с проницаемостью ε. Найти: 1) модуль вектора как функцию расстояния r от центра шара; 2) поверхностную и объемную плотности связанных зарядов.
Решение. 1) Для определения воспользуемся теоремой Гаусса для вектора , поскольку задано распределение лишь сторонних зарядов:
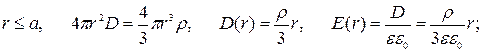
2) Поверхностная плотность связанного заряда
Для нахождения объемной плотности связанных зарядов достаточно повторить рассуждения, которые привели нас к формуле (2.9), и мы получим
2.5. Электроемкость уединенного проводника.
конденсаторы
Электроемкостью уединенного проводника (сокращенно емкостью) называют отношение заряда Q проводника к его потенциалу φпов:
. (2.14)
Электроемкость численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу. За единицу емкости принимают емкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл. Единица емкости - фарад, т.е. 
.
Электроемкость уединенного проводника зависит от его геометрических размеров, формы и диэлектрической проницаемости среды, окружающей его, и не зависит от заряда на проводнике.
Методические указания
Для нахождения емкости уединенного проводника необходимо:
1) мысленно зарядить данный проводник зарядом Q;
2) вычислить его потенциал φпов
— либо разбивая заряд Q на точечные dQ и применяя принцип суперпозиций: φпов = 
;
— либо предварительно рассчитав поле заряда Q (для случаев, когда можно применить теорему Гаусса), использовать связь между потенциалом и напряженностью El = 
и проинтегрировав найти φпов;
3) по формуле (1.1) рассчитать емкость.
Пример 2.3. Найти емкость уединенного проводника в вакууме, имеющего форму шара радиусом R.
Решение. Мысленно заряжаем шар зарядом Q и вычисляем его потенциал φпов. По теореме Гаусса поле шара, имеющего сферическую симметрию: 
, для r≥R. Потенциал шара (потенциал на бесконечности равен нулю):
.
После подстановки полученного выражения в (1.1) находим емкость уединенного шара
С=4πε0R.
Как видно из последнего выражения фарад – очень большая величина: емкостью 1 Ф обладал бы уединенный шар радиусом 9 млн. км, что в 1500 раз больше радиуса Земли (емкость Земли С = 0.7 мФ).
|
Пример 2.4. Найти емкость уединенного шарового проводника радиуса R1, окруженного прилегающим к нему концентрическим слоем однородного диэлектрика с диэлектрической проницаемостью ε и наружным радиусом R2 (рис. 10).
Рис. 10
Решение. Мысленно заряжаем шар зарядом Q и вычисляем его потенциал φпов = φ(R1). Вне и на поверхности проводника возникает электрическое поле. Расчет поля (оно имеет сферическую симметрию) можно провести по теореме Гаусса для вектора электрического смещения D:
ФD = D·4πr2 = Q, где R1 ≤ r ≤ R2.
Следовательно, напряженность поля в диэлектрике:
После интегрирования соотношения 
получаем распределение потенциала в диэлектрике:
.
Постоянную С находим из условия 
.
Таким образом, окончательное распределение потенциала в диэлектрике:
.
Используя условие непрерывности потенциала, определяем потенциал шарового проводника:
и его емкость:
Емкость конденсатора. Конденсатором называется совокупность двух (или нескольких) проводников, разделенных прослойкой диэлектрика. Это позволяет создать систему проводников, которая обладает емкостью, значительно большей, чем уединенный проводник, и притом не зависящий от окружающих тел. Простейший конденсатор состоит из двух проводников (обкладок) с одинаковыми по абсолютному значению, но противоположными по знаку зарядами (Q и -Q), расположенных на малом расстоянии друг от друга. Малое расстояние необходимо для того, чтобы внешние тела не оказывали влияния на емкость конденсатора и, поле было сосредоточено полностью внутри конденсатора.
Емкостью конденсатора называют отношение заряда одной из обкладок конденсатора Q к разности потенциалов между его обкладками (эту разность называют напряжением):
(2.15)
Емкость конденсатора зависит от его геометрии (размеров и формы обкладок), от зазора между ними и от заполняющей конденсатор среды.
При параллельном соединении конденсаторов (предварительно не заряженных) общая емкость С равна сумме соединяемых емкостей С1, С2, …, Сn:
(2.16)
При последовательном соединении конденсаторов (предварительно не заряженных) величина, обратная общей емкости, равна сумме величин, обратных соединяемым емкостям С1, С2, …, Сn:
(2.17)
Выражения для емкости некоторых конденсаторов между обкладками, которых находится однородный изотропный диэлектрик ε=const.
| Плоский конденсатор (d -расстояние между обкладками; S -площадь обкладки) | 
|
| Цилиндрический конденсатор, состоящий из двух коаксиальных обкладок радиусами r1 и r2 и высотой h. | 
|
| Сферический конденсатор, состоящий из двух концентрических обкладок радиусом r1 и r2. | 
|
Методические указания
