Указание. Воспользоваться симметрией системы зарядов и применить теорему Гаусса.
1.14. В безграничном плоском слое толщиной 2 d объемная плотность заряда ρ изменяется по закону ρ = ρ0 x/d (— d ≤ x ≤ d, где х — ось, перпендикулярная плоскости слоя. В слое имеется тонкий канал вдоль оси х, в котором помещен точечный диполь с массой m и дипольным моментом р. Вычислить период малых продольных колебаний диполя.
Потенциал электрического поля
1.15. Тонкое кольцо R =25 см. имеет заряд q =5,0 мкКл, неравномерно распределённый по кольцу. Найти работу электрических сил по перемещению точечного заряда q1 =10 мкКл из центра кольца по произвольному пути в точку, находящуюся на оси кольца на l =50 см от его центра.
1.16. Находящаяся в вакууме круглая тонкая пластинка радиуса R равномерно заряжена с поверхностной плотностью s. Найти потенциал и модуль напряженности электрического поля на оси пластинки как функцию расстояния l от ее центра.
1.17.Коническая поверхность с основанием радиуса R и углом между боковой поверхностью и прямой, соединяющей центр основания и вершину β, равномерно заряжена с поверхностной плотностью s. Найти потенциал в вершине конуса.
1.18. Два коаксиальных кольца, каждое радиуса R, из тонкой проволоки находятся на малом расстоянии l друг от друга (l<<R) и имеют заряды q и –q. Найти потенциал и напряженность электрического поля на оси системы как функции координаты
1.19. Потенциал поля внутри заряженного шара зависит только от расстояния до его центра как  , где
, где  и
и 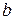 — постоянные. Найти распределение объёмного заряда
— постоянные. Найти распределение объёмного заряда  внутри шара.
внутри шара.
2. Проводники и диэлектрики в электрическом поле
При внесении любого вещества в электрическое поле в веществе происходит смещение положительных и отрицательных зарядов (ядер и электронов), что в свою очередь приводит к частичному разделению этих зарядов. В тех или иных местах вещества появляются нескомпенсированные заряды различного знака. Это явление называют электростатической индукцией, а появившиеся в результате разделения заряды — индуцированными зарядами.
Индуцированные заряды создают дополнительное электрическое поле, которое вместе с исходным (внешним) электрическим полем образует результирующее поле. Зная внешнее поле и распределение индуцированных зарядов, можно при нахождении результирующего поля уже не обращать внимания на наличие самого вещества — его роль уже учтена с помощью индуцированных зарядов.
Таким образом, результирующее поле при наличии вещества определяется просто как суперпозиция внешнего поля и поля индуцированных зарядов. Однако во многих случаях дело усложняется тем, что мы заранее не знаем, как распределяются в пространстве все эти заряды — задача оказывается далеко не такой простой, как могло бы показаться вначале. Как мы увидим далее, распределение индуцированных зарядов в решающей степени зависит от свойств самого вещества — от его физической природы и формы тел.
2.1. Поле внутри и снаружи проводника, помещенного в электростатическое поле
Внутри проводника Е = 0. Поместим металлический проводник во внешнее электростатическое поле или сообщим ему какой-нибудь заряд. В обоих случаях на все заряды проводника будет действовать электрическое поле, в результате чего все отрицательные заряды (электроны) сместятся против поля. Такое перемещение зарядов (ток) будет продолжаться до тех пор (практически это происходит в течение малой доли секунды), пока не установится определенное распределение зарядов, при котором электрическое поле во всех точках внутри проводника обратится в нуль. Таким образом, в статическом случае электрическое поле внутри проводника отсутствует (Е = 0).
Избыточные заряды появляются лишь на поверхности проводника с некоторой плотностью а, вообще говоря, различной в разных точках его поверхности. Заметим, что избыточный поверхностный заряд находится в очень тонком поверхностном слое (его толщина около одного-двух межатомных расстояний).
Отсутствие поля внутри проводника означает согласно (1.31), что потенциал φ в проводнике одинаков во всех его точках, т. е. любой проводник в электростатическом поле представляет собой эквипотенциальную область и его поверхность является эквипотенциальной.
Поверхность проводника эквипотенциальна и непосредственно у этой поверхности поле  направлено по нормали к ней в каждой точке. Если бы это было не так, то под действием касательной составляющей
направлено по нормали к ней в каждой точке. Если бы это было не так, то под действием касательной составляющей  заряды пришли бы в движение по поверхности проводника, т. е. равновесие зарядов было бы невозможным.
заряды пришли бы в движение по поверхности проводника, т. е. равновесие зарядов было бы невозможным.
Поле у поверхности проводника. Напряженность электрического поля непосредственно у поверхности проводника связана с поверхностной плотностью заряда на поверхности проводника. Эту связь молено легко установить с помощью теоремы Гаусса.
Пусть интересующий нас участок поверхности проводника граничит с вакуумом. Линии вектора  перпендикулярны поверхности проводника, поэтому в качестве замкнутой поверхности возьмем небольшой цилиндр. Тогда поток вектора
перпендикулярны поверхности проводника, поэтому в качестве замкнутой поверхности возьмем небольшой цилиндр. Тогда поток вектора  через эту поверхность будет равен только потоку через «наружный» торец цилиндра (потоки через боковую поверхность и внутренний торец равны нулю), и мы имеем EnΔS = σΔS/ε0, где En — проекция вектора
через эту поверхность будет равен только потоку через «наружный» торец цилиндра (потоки через боковую поверхность и внутренний торец равны нулю), и мы имеем EnΔS = σΔS/ε0, где En — проекция вектора  на внешнюю нормаль
на внешнюю нормаль  (по отношению к проводнику), ΔS — площадь сечения цилиндра, σ — локальная поверхностная плотность заряда на проводнике. Сократив обе части этого равенства на ΔS, получим
(по отношению к проводнику), ΔS — площадь сечения цилиндра, σ — локальная поверхностная плотность заряда на проводнике. Сократив обе части этого равенства на ΔS, получим

|
En = σ/ε0. (2.1)
Если σ > 0, то и En > О, т. е. вектор  направлен от поверхности проводника — совпадает по направлению с нормалью
направлен от поверхности проводника — совпадает по направлению с нормалью  ; если же σ < 0, то En < О — вектор
; если же σ < 0, то En < О — вектор  направлен к поверхности проводника.
направлен к поверхности проводника.
Силы, действующие на поверхность проводника. Рассмотрим случай, когда заряженный участок поверхности проводника граничит с вакуумом. На малый элемент ΔS поверхности проводника действует сила
 (2.2)
(2.2)
где σΔS —заряд этого элемента, 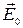 — напряженность поля, создаваемого всеми остальными зарядами системы в месте нахождения заряда σΔS.
— напряженность поля, создаваемого всеми остальными зарядами системы в месте нахождения заряда σΔS. 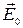 не равно напряженности
не равно напряженности  поля вблизи данного элемента поверхности проводника, однако между ними имеется простая связь. Пусть
поля вблизи данного элемента поверхности проводника, однако между ними имеется простая связь. Пусть  — напряженность поля, создаваемого зарядом на площадке ΔS в точках, очень близких к этой площадке — здесь она ведет себя как бесконечная равномерно заряженная плоскость. Тогда
— напряженность поля, создаваемого зарядом на площадке ΔS в точках, очень близких к этой площадке — здесь она ведет себя как бесконечная равномерно заряженная плоскость. Тогда  = σ / ε0.
= σ / ε0.
 
  S S
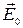 
 Рис.9
Рис.9
|
Результирующее поле как внутри, так и вне проводника (вблизи площадки ΔS) является суперпозицией полей 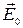 и
и  . По разные стороны площадки ΔS поле
. По разные стороны площадки ΔS поле 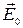 практически одинаково, поле же
практически одинаково, поле же  имеет противоположные направления (рис. 9, где для определенности взято σ > 0). Из условия
имеет противоположные направления (рис. 9, где для определенности взято σ > 0). Из условия  = 0 в проводнике следует, что
= 0 в проводнике следует, что 
 , тогда снаружи проводника у его поверхности Е=Е0+Еσ=2Е0. Итак,
, тогда снаружи проводника у его поверхности Е=Е0+Еσ=2Е0. Итак,
 ,
,
и уравнение (2.2) примет вид:

Разделив обе части этого уравнения на ΔS, получим выражение для силы, действующей на единицу поверхности проводника
 (2.3)
(2.3)
где  — внешняя нормаль к элементу поверхности в данной точке проводника. Величину
— внешняя нормаль к элементу поверхности в данной точке проводника. Величину  называют поверхностной плотностью сил. Независимо от знака σ, а значит, и направления
называют поверхностной плотностью сил. Независимо от знака σ, а значит, и направления  , сила
, сила  всегда направлена, как видно из (2.3), наружу проводника, стремясь его растянуть.
всегда направлена, как видно из (2.3), наружу проводника, стремясь его растянуть.
2.2. Общая задача электростатики. Метод изображений
Очень часто приходится встречаться с задачами, в которых распределение зарядов неизвестно, но заданы потенциалы проводников, их форма и относительное расположение. Требуется определить потенциал  в любой точке поля между проводниками. Зная
в любой точке поля между проводниками. Зная  , можно легко восстановить само поле
, можно легко восстановить само поле  и по значению
и по значению  непосредственно у поверхности проводников найти распределение поверхностных зарядов на них.
непосредственно у поверхности проводников найти распределение поверхностных зарядов на них.
Уравнения Пуассона и Лапласа. Найдем дифференциальное уравнение, которому должна удовлетворять функция φ — потенциал. Для этого подставим в левую часть (1.12) вместо  его выражение через φ, т. е.
его выражение через φ, т. е. 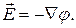 В результате получим общее дифференциальное уравнение для потенциала — уравнение Пуассона:
В результате получим общее дифференциальное уравнение для потенциала — уравнение Пуассона:
 (2.4)
(2.4)
где  — оператор Лапласа (лапласиан). В декартовых координатах он имеет вид
— оператор Лапласа (лапласиан). В декартовых координатах он имеет вид

Если между проводниками нет зарядов (ρ = 0), то уравнение (2.4) переходит в более простое — уравнение Лапласа:
 (2.5)
(2.5)
Определение потенциала сводится к нахождению такой функции φ, которая во всем пространстве между проводниками удовлетворяет уравнениям (2.4) или (2.5), а на поверхностях самих проводников принимает заданные значения φ1, φ2 и т.д.
В теории доказывается, что эта задача имеет единственное решение. Это утверждение называют теоремой единственности. По теореме единственности можно также утверждать, что заряд на поверхности проводника в статическом случае распределяется тоже единственным образом. Действительно, между зарядами на проводнике и электрическим полем вблизи его поверхности имеется однозначная связь. Отсюда сразу и следует, что единственность поля  определяет и единственность распределения заряда на поверхности проводника.
определяет и единственность распределения заряда на поверхности проводника.
Решение уравнений (2.4) и (2.5) в общем случае — задача сложная и кропотливая. Аналитические решения этих уравнений получены лишь для немногих частных случаев. Использование же теоремы единственности весьма облегчает решение ряда электростатических задач. Если решение задачи удовлетворяет уравнению Лапласа (или Пуассона) и граничным условиям, то можно утверждать, что оно является правильным и единственным, каким бы способом (хотя бы путем догадки) мы ни нашли его.
Метод изображений. Это искусственный метод, позволяющий в ряде частных случаев рассчитать электрическое поле достаточно просто. Рассмотрим идею этого метода на самом простом примере, когда точечный заряд q находится около безграничной проводящей плоскости (рис. 9, а).
Идея метода заключается в том, что мы должны найти другую задачу, которая решается просто и решение которой или часть его может быть использовано. В нашем случае такой простой задачей является задача с двумя зарядами q и -q. Поле этой системы известно (его линии вектора Е показаны на рис. 9, б).
Совместим со средней эквипотенциальной поверхностью (ее потенциал  = 0) проводящую плоскость и уберем заряд -q. Согласно теореме единственности поле в верхнем полупространстве останется прежним. Действительно, на проводящей плоскости и всюду в бесконечности
= 0) проводящую плоскость и уберем заряд -q. Согласно теореме единственности поле в верхнем полупространстве останется прежним. Действительно, на проводящей плоскости и всюду в бесконечности  = 0, точечный же заряд q можно рассматривать как предельный случай малого сферического проводника, радиус которого стремится: к нулю, а потенциал — к бесконечности. Таким образом, в верхнем полупространстве граничные условия для потенциала остались теми же, стало быть, тем же осталось и поле в этой области (рис. 9, в).
= 0, точечный же заряд q можно рассматривать как предельный случай малого сферического проводника, радиус которого стремится: к нулю, а потенциал — к бесконечности. Таким образом, в верхнем полупространстве граничные условия для потенциала остались теми же, стало быть, тем же осталось и поле в этой области (рис. 9, в).

|

|

|
а) б) в)
Рис.9
Итак, в рассматриваемом случае поле отлично от нуля только в верхнем полупространстве, и для вычисления этого поля достаточно ввести фиктивный заряд-изображение q' = -q, противоположный по знаку заряду q, поместив его по другую сторону проводящей плоскости на таком же расстоянии от нее, что и заряд q. Фиктивный заряд q создает в верхнем полупространстве точно такое же поле, как и индуцированные заряды на плоскости. Именно это подразумевают, когда говорят, что фиктивный заряд заменяет собой «действие» всех индуцированных зарядов. Надо только иметь в виду, что «действие» фиктивного заряда распространяется лишь на то полупространство, в котором находится действительный заряд q. В другом полупространстве поле отсутствует.
Можно сказать, что метод изображений по существу основан на подгонке потенциала под граничные условия: мы стараемся найти другую задачу (конфигурацию зарядов), у которой конфигурация поля в интересующей нас части пространства была бы той же. Если это удается сделать с помощью достаточно простых конфигураций, то метод изображений оказывается весьма эффективным.
2.3. Поле в диэлектрике. Основные характеристики
Диэлектриками (или изоляторами) называют вещества, практически не проводящие электрического тока. Это значит, что в диэлектриках в отличие, например, от проводников нет зарядов, способных перемещаться на значительные расстояния, создавая ток.
При внесении даже нейтрального диэлектрика во внешнее электрическое поле обнаруживаются существенные изменения, как в поле, так и в самом диэлектрике; последнее следует хотя бы из того, что на диэлектрик начинает действовать сила, увеличивается емкость конденсатора при заполнении его диэлектриком и др.
Диэлектрики состоят либо из нейтральных молекул, либо из заряженных ионов, находящихся в узлах кристаллической решетки (ионные кристаллы, например, типа NaCl). Сами же молекулы могут быть полярными и неполярными. У полярных молекул центр «тяжести» отрицательного заряда сдвинут относительно центра тяжести положительных зарядов, в результате чего они обладают собственным дипольным моментом. Неполярные же молекулы собственным дипольным моментом не обладают: у них центры тяжести положительного и отрицательного зарядов совпадают.
Поляризация. Под действием внешнего электрического поля происходит поляризация диэлектрика. Это явление заключается в следующем. Если диэлектрик состоит из неполярных молекул, то в пределах каждой молекулы происходит смещение зарядов — положительных по полю, отрицательных против поля. Если же диэлектрик состоит из полярных молекул, то при отсутствии внешнего поля их дипольные моменты ориентированы совершенно хаотически (из-за теплового движения). Под действием же внешнего поля дипольные моменты ориентируются преимущественно в направлении внешнего поля. Наконец, в диэлектрических кристаллах типа NaCl при включении внешнего поля все положительные ионы смещаются по полю, отрицательные — против поля.
Механизм поляризации связан с конкретным строением диэлектрика. Однако для дальнейшего существенно лишь то, что независимо от механизма поляризации в этом процессе все положительные заряды смещаются по полю, а. отрицательные — против поля. Смещения зарядов в обычных условиях весьма малы даже по сравнению с размерами молекул, это связано с тем, что напряженность внешнего поля, действующего на диэлектрик, значительно меньше напряженности внутренних электрических полей в молекулах.
В результате поляризации на поверхности диэлектрика, а также, и в его объеме появляются нескомпенсированные заряды. Нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называют поляризационными или связанными (свобода перемещения таких зарядов ограничена). Связанные заряды будем отмечать штрихом (q', ρ', σ').
Заряды, которые не входят в состав молекул диэлектрика, называют сторонними. Эти заряды могут находиться как внутри, так и вне диэлектрика.
Полем  в диэлектрике мы будем называть величину, являющуюся суперпозицией поля
в диэлектрике мы будем называть величину, являющуюся суперпозицией поля 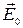 сторонних зарядов и поля
сторонних зарядов и поля  связанных зарядов:
связанных зарядов:
 =
= 
 . (2.5)
. (2.5)
Поляризованность Р. Для количественного описания поляризации диэлектрика естественно взять дипольный момент единицы объема. Если внешнее поле или диэлектрик (или то и другое) неоднородны, степень поляризации оказывается различной в разных точках диэлектрика. Чтобы охарактерирозовать поляризацию в данной точке, мысленно выделяют физически бесконечно малый объем ΔV, содержащий эту точку, затем находят векторную сумму дипольных моментов молекул в этом объеме и составляют отношение
 (2.5)
(2.5)

|
Этот вектор  , численно равный дипольному моменту единицы объема вещества называют поляризованностъю диэлектрика. Единицей поляризованности
, численно равный дипольному моменту единицы объема вещества называют поляризованностъю диэлектрика. Единицей поляризованности  является кулон на квадратный метр (Кл/м2).
является кулон на квадратный метр (Кл/м2).
Как показывает опыт, для обширного класса диэлектриков и широкого круга явлений поляризованность  зависит линейно от напряженности
зависит линейно от напряженности  поля в диэлектрике. Если диэлектрик изотропный и
поля в диэлектрике. Если диэлектрик изотропный и  не слишком велико, то
не слишком велико, то
 (2.6)
(2.6)
где α — безразмерная величина, называемая диэлектрической восприимчивостью вещества. Эта величина не зависит от  , она характеризует свойства самого диэлектрика. Всегда α > 0.
, она характеризует свойства самого диэлектрика. Всегда α > 0.
Существуют, однако, и диэлектрики, для которых (2.6) не применимо. Это некоторые ионные кристаллы и электреты, а также сегнетоэлектрики. У сегнетоэлектриков связь между  и
и  нелинейная и зависит от предшествующих значений
нелинейная и зависит от предшествующих значений  (это явление называют гистерезисом).
(это явление называют гистерезисом).
2.4. Теорема Гаусса для векторов  ,
,  и
и 
Теорема Гаусса для поля вектора Р. Поток вектора  сквозь произвольную замкнутую поверхность S равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью S
сквозь произвольную замкнутую поверхность S равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью S
 (2.7)
(2.7)
Это уравнение называется теоремой Гаусса для вектора 

|

|
В дифференциальной форме уравнение (2.7) — теорема Гаусса для поля вектора  — имеет следующий вид:
— имеет следующий вид:
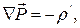 (2.8)
(2.8)
т. е. дивергенция поля вектора  равна с обратным знаком объемной плотности избыточного связанного заряда в той же точке.
равна с обратным знаком объемной плотности избыточного связанного заряда в той же точке.
На основании теоремы Гаусса для вектора  (2.7) можно показать, что объемная плотность избыточных связанных зарядов внутри диэлектрика будет равна нулю при одновременном выполнении двух условий:
(2.7) можно показать, что объемная плотность избыточных связанных зарядов внутри диэлектрика будет равна нулю при одновременном выполнении двух условий:
1) диэлектрик должен быть однородным;
2) внутри него не должно быть сторонних зарядов (ρ = 0). Действительно, в выражении (2.7) в случае однородного диэлектрика можно, заменив  на
на  согласно (2.6), вынести α из-под знака интеграла и записать:
согласно (2.6), вынести α из-под знака интеграла и записать:

Оставшийся интеграл есть не что иное, как алгебраическая сумма всех зарядов — сторонних и связанных — внутри рассматриваемой замкнутой поверхности S, т. е. q + q'. Поэтому
 (2.9)
(2.9)

|

|
Это соотношение между избыточным связанным зарядом q' и сторонним зарядом q справедливо для любого объема внутри диэлектрика, в частности и для физически бесконечно малого

Отсюда следует, что в однородном диэлектрике ρ' = 0, когда ρ = 0. Таким образом, если в произвольное электрическое поле поместить однородный изотропный диэлектрик какой угодно формы, можно быть уверенным, что при его поляризации появятся только поверхностные связанные заряды, объемные же избыточные связанные заряды во всех точках такого диэлектрика будут равны нулю.
Вектор D. Поскольку источниками поля  являются все электрические заряды — сторонние и связанные, теорему Гаусса для поля
являются все электрические заряды — сторонние и связанные, теорему Гаусса для поля  можно записать так:
можно записать так:
 (2.10)
(2.10)
где q и q' — сторонние и связанные заряды, охватываемые поверхностью S.
Появление связанных зарядов q усложняет дело, и формула (2.10) оказывается малополезной для нахождения поля  в диэлектрике даже при «достаточно хорошей» симметрии. Действительно, эта формула выражает свойства неизвестного поля
в диэлектрике даже при «достаточно хорошей» симметрии. Действительно, эта формула выражает свойства неизвестного поля  через связанные заряды q', которые в свою очередь определяются неизвестным полем
через связанные заряды q', которые в свою очередь определяются неизвестным полем  .
.
Это затруднение, однако, можно обойти, если выразить заряд q' через поток вектора  по формуле (2.7). Тогда выражение (2.10) можно преобразовать к виду:
по формуле (2.7). Тогда выражение (2.10) можно преобразовать к виду:
 (2.11)
(2.11)
Вспомогательный вектор  определяемый соотношением
определяемый соотношением
 (2.12)
(2.12)
называется электрическим смещением, а выражение (2.11) теоремой Гаусса для вектора  : поток которого сквозь произвольную замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.
: поток которого сквозь произвольную замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.






