Использованный в работе способ определения электроемкости основан на том, что при зарядке конденсатора напряжение между его обкладками U (t) достигает своего максимального значения, равного напряжению источника U 0, не мгновенно, а возрастая по экспоненциальному закону (рис. 1).
Время полной зарядки конденсатора зависит от его емкости. Если время зарядки 
выбрать таким образом, чтобы оно не превышало времени 80 - 90 % от зарядки наименьшей из измеряемых емкостей, то при этом напряжения между обкладками (U 1 и U 2, рис. 1) однозначно связаны с емкостью конденсаторов.
Следовательно, зарегистрировав значение U (t*) и установив аналитическую связь параметров U (t*) и C, можно определить неизвестную электроемкость C.
Для вывода расчетной формулы используем схему, представленную на рис. 2. Конденсатор C заряжается от источника постоянного напряжения U 0. Ток, текущий через сопротивление R в любой момент времени t, по закону Ома будет равен:
, (1)
где U (t) - напряжение между обкладками конденсатора, величина которого прямо пропорциональна накопленному им за время t заряду q (t) и 
. Продифференцируем это выражение по времени: 
. Так как 
, определим ток, текущий через конденсатор в момент времени t:
. (2)
Сила тока I (t) пропорциональна не напряжению (как в случае закона Ома для сопротивления), а скорости изменения напряжения на конденсаторе.
Из выражений (1) и (2) (величина I (t) в обоих уравнениях одинакова), следует:
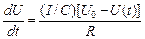, или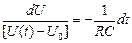 
.
Решение этого дифференциального уравнения:
.
Постоянную A определим из начальных условий: при t = 0 напряжение U (t) = 0, тогда A = - U 0. Таким образом, напряжение на конденсаторе увеличивается по закону (см. рис.1):
. (3)
Из уравнения (3): 
, или
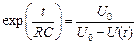. (4)
Прологарифмировав выражение (4), получим:
,
откуда выразим измеряемую ёмкость:
.
Окончательно для фиксированного момента времени , получим:
, (5)
здесь k = t */ R, а величины U 0, R и t * являются постоянными установки. Значение U 0 указано на лицевой панели прибора.
Из рабочей формулы (5) следует, что постоянную k можно определить, измерив напряжение U (t *) конденсатора известной емкости C 0.
