3. Рассмотрим электрическую цепь, состоящую из источника переменного тока и конденсатора (рис. 17.3). В этой цепи по проводам течет переменный ток, потому что половину периода конденсатор накапливает заряды и заряжается, а вторую половину периода разряжается. Но внутри конденсатора свободные заряды отсутствуют и тока проводимости нет.
При протекании тока около проводников возникает магнитное поле. Индукцию магнитного поля можно определить по закону полного тока для некоторого контура, охватывающего проводник 
. Здесь сумма токов пронизывает произвольную поверхность, ограниченную контуром. Если эта поверхность диск, то ток проводника его пересекает и индукцию магнитного поля можно определить. А если эта поверхность в форме цилиндра, дно которого внутри конденсатора, то его поверхность токи не пересекают, и магнитного поля нет. Возникает парадокс.
Максвелл предложил гипотезу, что внутри конденсатора течет так называемый ток смещения. Предполагалось, что он обусловлен смещением связанных зарядов диэлектрика. Но как быть, если между обкладками вакуум? По гипотезе Максвелла ток смещения обусловлен не зарядами, а изменением электрического поля конденсатора.
Ток смещения замыкает ток проводимости и равен ему. Сила тока в цепи, по определению, равна скорости изменения заряда конденсатора: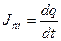 
. Поверхностная плотность заряда на обкладках равна вектору смещения электрического поля конденсатора. Тогда заряд связан с параметром электрического поля 
. Сила тока смещения равна.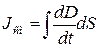 
. Добавив ток смещения в общем случае к току проводимости, преобразуем закон полного тока во второе уравнение Максвелла
. 17.3
Циркуляция вектора индукции магнитного поля равна алгебраической сумме токов проводимости и тока смещения электрического поля сквозь поверхность, ограниченную контуром.
В скобке стоит сумма плотности тока проводимости и плотности тока смещения. Для нахождения направления вектора индукции магнитного поля, созданного током смещения, справедливо правило буравчика, который надо вворачивать в направлении тока смещения, то есть в направлении возрастания вектора смещения электрического поля.
