5. КПД подстанции. Применение пускового реостата и трех схем включения двигателей позволяет сэкономить электрическую энергию. Пусть, например, имеется всего одна схема включения двигателей – параллельная. Пусть в режиме движения поезда при ограничении силы тяги по сцеплению, сила тяги равна предельной силе сцепления и почти постоянна. Также остается постоянной сила тока J max. Это достигается регулированием сопротивления реостата, которое должно быть много больше обычного. За время разгона t 0 тяговая подстанция совершит работу, которая равна произведению мощности на время разгона: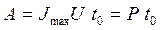 
. На графике "мощность–время" работа подстанции равна площади прямоугольника с ординатой Р и абсциссой t 0 (рис. 13.4). Работа подстанции расходуется на полезную работу двигателей локомотива и на теплоту, выделяемую на пусковом реостате.
Полезная мощность локомотива равна произведению силы тяги на скорость, а при постоянном ускорении скорость пропорциональна времени разгона: 
. На графике P (t) это прямая линия, являющаяся диагональю прямоугольника. Полезная работа по графическому смыслу интеграла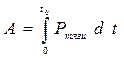 
равна площади треугольника 
. Площадь треугольника в два раза меньше площади прямоугольника. Значит, в режиме разгона с одной схемой включения двигателей только половина работы тяговой подстанции превращается в механическую энергию поезда. Остальная работа превращается в теплоту на пусковом реостате. КПД режима разгона с одной схемой включения двигателей 50%.
Если используется три схемы включения тяговых двигателей, каждая со своим напряжением, то выделенная теплота будет равна площади трех заштрихованных треугольников, или трех маленьких прямоугольников (рис. 16.4). В то время как полная работа тяговой подстанции равна площади большого прямоугольника, или 16 маленьких. Тогда доля потерь будет равна 3/16, а КПД η =13/16 = 81,5%. Если бы схем включения двигателей было больше трех, то тепловые потери в режиме разгона при постоянной силе тяги были бы еще меньше.
Контрольные вопросы
1. Как изменяется суммарная сила тока тяговых двигателей локомотива при переключении трех схем соединения восьми тяговых двигателей локомотива, если в режиме разгона сила тяги колес постоянна?
2. Если у локомотива шесть тяговых двигателей, то какие схемы соединения тяговых двигателей возможны? В каком соотношении находятся предельные значения сил токов локомотива?
3. Как изменяется суммарная сила тяги и потребляемая мощность локомотива в режиме ограничения по сцеплению колес при увеличении скорости движения поезда.
4. По какому закону изменяется сила тяги локомотива в режиме движения при постоянной мощности? Как при этом изменяется сила потребляемого тока?
5. Запишите закон Ома для электрической железной дороги в первый момент трогания поезда.
6. Запишите уравнение для скорости равномерного движения поезда в режиме при постоянной мощности двигателей.
7. Почему шунт катушки возбуждения в режиме «ослабления возбуждения» должен обладать индуктивностью? Почему не применить простой реостат?
8. Зависит ли противо-ЭДС якорной обмотки от силы тока, потребляемого коллекторным двигателем?
9. Что произойдет, если машинист вместо одной ступени пускового реостата отключит сразу две?
10. Что произойдет, если машинист вместо отключения ступени реостата повернет контроллер в обратную сторону и добавит сопротивление реостата?
11. Определите КПД тяговой подстанции в режиме разгона при постоянной силе тяги, если локомотив имеет шесть тяговых двигателей.
12. Определите КПД тяговой подстанции в режиме разгона при постоянной силе тяги, если трамвай имеет один тяговы1 двигатель.
13. Сколько значений скорости равномерного движения имеет троллейбус с одним тяговым двигателей? Как регулируется скорость движения?
14. Сколько значений скорости равномерного движения имеет поезд, если у локомотива шесть тяговых двигателей и три ступени ослабления возбуждения?
15. Плоскость витка якорной обмотки параллельна силовым линиям магнитного поля катушек возбуждения. По витку протекает электрический ток. Как направлено магнитное поле витка?
16. Как направлено магнитное поле электрического тока якорной обмотки по отношению к магнитному полю катушек возбуждения?
17. Пусть пусковой реостат состоит из трех резисторов с разными сопротивлениями. Сколько ступеней регулирования может иметь такой реостат?
18. Сопротивления обмоток тягового электродвигателя равно 0,02 Ом. Если включить тяговые двигатели локомотива при параллельном соединении без пускового реостата к подстанции, то какой ток потечет по обмоткам?
19. По какому закону уменьшается сила тяги локомотива при движении с постоянной мощностью двигателей? Почему с ила тяги уменьшается?
20. При движении поезда при разгоне началось буксование колес локомотива. Каковы возможные причины буксования? На что тратится работа тяговой подстанции?
14. МОЩНОСТЬ И СИЛА ТОКА ЭЛЕКТРОВОЗА
1. Для электрической железной дороги выполняется закон Ома. Напряжение подстанции равно сумме противо-ЭДС двигателей и потере напряжения на проводах контактной сети и обмоток двигателя: 
. Однако определить силу тока в контактной сети непосредственно по уравнению закона Ома невозможно. Это обусловлено тем, что противо-ЭДС не постоянна, а зависит от индукции магнитного поля В: 
для одного двигателя. В двигателях последовательного возбуждения противо-ЭДС будет зависеть от силы тока двигателя точно также как и индукция (рис. 14.1). Суммарную противоЭДС двигателей локомотива определяют сложением ЭДС отдельных двигателей в зависимости от схемы соединения двигателей.
Возможно графическое решение уравнения закона Ома. Пусть для простоты двигатели электровоза при равномерном движении вращаются с постоянной угловой скоростью ω. Проведем на графике (рис. 14.1) прямые линии 
. Абсциссы точек пересечения с линией ЭДС всех двигателей локомотива дадут расчетное значение силы потребляемого тока. Так как сопротивление контактной сети зависит от расстояния между подстанцией и электровозом l > 0, то с удалением от подстанции угол наклона линии 
будет возрастать, точка пересечения будет смещаться в диапазон малых токов. Определив силу тока, можно определить мощность тяговых двигателей как площадь прямоугольника (P=εJ) на графике.
2. На стадии проектирования электровоза необходимую силу токаможноопределить по заданной мощности тяговых двигателей. Зависимость полезной мощности тяговых двигателей от силы тока, согласно уравнению баланса мощности, определяется уравнением второго порядка
. 14.1
Функция мощности имеет максимум (рис.14.2). Приравняв первую производную к нулю 
, получим значение силы тока, при котором полезная мощность принимает максимальное значение
. 14.2
Это в два раза меньше тока короткого замыкания, когда якоря двигателей не вращаются, противоЭДС отсутствует. Однако работать в этом режиме тяговые двигатели не должны, так как коэффициент полезного действия подстанции 
слишком мал, равен 50 %.
Решая квадратное уравнение баланса мощности, подставив в него J maxи приведя к виду 
можно определить силу тока, потребляемую двигателями локомотива. Это уравнение второго порядка относительно силы тока и его решение имеет два корня:
. (14.3)
Если корни действительные и положительные, то двигатели локомотива выбирают меньший ток J 1. Если корни мнимые, то тяговая подстанция не в состоянии обеспечить заданную мощность тяговых двигателей локомотива из-за большого сопротивления контактной сети. Следует или увеличивать сечение проводов контактной сети, или уменьшать расстояние между подстанциями.
Однако на рассчитанное предельное значение силы тока тяговых двигателей накладываются несколько ограничений, которые нельзя превышать. Сила тока не может быть настолько большой, чтобы ведущие колеса локомотива буксовали (см. формулу 13.1: 
). Необходимо, чтобы КПД подстанции был не менее 95%, необходимо, чтобы не перегревались двигатели, не перегревался провод.
3. Потребуем, чтобы КПД тяговой подстанции был не менее η= 95%, то есть тепловые потери не превышали 5% от потребляемой мощности. По закону Джоуля –Ленца мощность тепловых потерь равна произведению квадрата силы тока на сопротивление 
. Отсюда допустимая сила тока по ограничению потерь мощности равна
. 14.4
Расчетная сила тока по этой формуле не должна превышать силу тока формуле 14.2, иначе КПД железной дороги будет мал.
Исключим из закона Джоуля-Ленца силу тока по формуле КПД подстанции 
. Мощность тепловых потерь будет равна
14.5
Как видно из формулы, для снижения тепловых потерь, следует, во-первых, уменьшать сопротивление проводов контактной сети. По формуле 
нужно увеличить площадь сечения, но это приведёт к утяжелению проводов, удорожанию контактной сети. Или следует уменьшать длину контактного провода, то есть уменьшать расстояние между подстанциями.
Во-вторых, можно повысить напряжение контактной сети. Например, при повышении напряжения тяговой подстанции в два раза, сила тока уменьшится в два раза, а тепловые потери в четыре раза при постоянном сечении проводов. Поэтому существуют предложения повысить напряжение в контактной сети постоянного тока вместо 3 кВ до 6 кВ и даже до 12 кВ. По этой же причине применяется контактная сеть переменного тока с напряжением 25 и 50 кВ.
Определим сопротивление контактного провода между ближайшими подстанциями при заданной мощности электровоза Р. Решая уравнение баланса мощности относительно сопротивления контактного провода, получим
. (14.6)
По этой формуле при мощности двигателей несколько МВт величина сопротивления контактной сети должна составлять 0,2–0,3 ом. Тогда расстояние между подстанциями при площади сечении провода 200 мм2 будет около 20 км.
4. Ограничение силы тока по нагреву двигателей. В процессе работы электродвигатели нагреваются вследствие выделения теплоты на активном сопротивлении обмоток возбуждения и обмоток якоря и потерь на гистерезис при перемагничивании железа якоря. Это может привести к перегреву двигателя. Теплота, выделяемая за некоторое малое время, dQ = J 2 r dt, расходуется на теплоотдачу окружающей среде и нагрев двигателя.
Нагрев приводит к повышению температуры двигателя аккумулированной теплотой 
. Здесь m – масса двигателя, с – удельная теплоемкость материала (в основном это сталь), dT – повышение температуры. Теплоотдача окружающей среде пропорциональна площади теплоотдающей поверхности двигателя S и перепаду температур (Т-Т0) между поверхностью двигателя и окружающей средой: dQотд = α S (T–T0) dt. Здесь α – коэффициент теплоотдачи, зависящий от способа теплоотдачи. Запишем уравнение теплового баланса
14.7
Произведем расчет температуры двигателя в зависимости от времени работы. Пусть сила тока постоянна. Разделим в дифференциальном уравнении (14.7) переменные: время t и температуру T. В результате получим 
. Проинтегрируем обе части уравнения в пределах: по времени от нуля до текущего момента t, по температуре от начальной Т0 до текущей температуры Т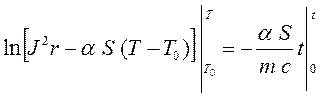 
. Подставим пределы интегрирования и потенцируя, получим зависимость температуры корпуса двигателя от времени
14.8
Температура корпуса растет со временем по экспоненциальному закону (рис.14.3). Скорость роста определяется коэффициентом показателя экспоненты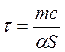 
. Это так называемое время релаксации. Чем больше масса и удельная теплоемкость двигателя, тем дольше по времени нарастает температура. В пределе, при бесконечно долгом времени работы температура стремится к равновесному значению. При этом температура корпуса становится предельной, а вся подводимая теплота рассеивается в пространство
. 14.9
Существует допустимая температура эксплуатации тяговых двигателей. Она ограничивает допустимое время работы двигателя. Чем выше сила тока, тем меньше допустимое время работы двигателя (рис. 14.3). Поэтому для увеличения длительности безопасной работы двигателя, чтобы доехать без остановки до следующей станции, приходится ограничивать силу потребляемого тока и мощность двигателей. Существует понятие «часовой режим» при котором в течении часа не допускается перегрева двигателей. По этому режиму определяется номинальная, паспортная мощность тяговых двигателей и допустимая сила тока.
Контрольные вопросы
1. Как по графику (рис. 14.1) определить мощность тяговой подстанции, мощность двигателя и мощность тепловых потерь при заданном сопротивлении контактной сети и двигателей?
2. Как можно рассчитать сопротивление контактной сети?
3. Почему тяговые подстанции переменного тока располагаются на расстоянии друг от друга в три раза дальше, чем тяговые подстанции постоянного тока?
4. Почему электроэнергия от электростанций к потребителю передается под высоким напряжением в несколько сотен киловольт?
5. Возможен ли переход к повышению напряжения контактной сети постоянного тока до 6 или 12 кВ? С какой целью это предлагается?
6. Каким образом может осуществляется импульсное регулирование мощности тяговых двигателей? Как будет влиять на процессы переключения явление самоиндукции?
7. Почему индукция магнитного поля в железе магнитной цепи электродвигателя при беспредельном увеличении силы тока в катушках возбуждения достигает насыщения?
8. Какие способы можно придумать для принудительного охлаждения перегревшегося тягового двигателя?
9. Когда быстрее растет температура двигателя: в начале работы или в конце? Когда быстрее остывает двигатель: в начале охлаждения или в конце? Теоретически сколько времени будет остывать неработающий двигатель?
10. При каких условиях электрический двигатель может сколь угодно долго работать без перегрева?
11. Какой двигатель, большой мощности или маленькой, более склонны к перегреву?
12. Почему из двух значений силы тока для получения одной и той же мощности реализуется меньшее значение?
13. Какие меры следует предпринять, чтобы из двигателя «выжать» максимальную мощность? Каков коэффициент полезного действия двигателя в режиме максимальной мощности?
14. Что произойдет с ведущим колесом электровоза, если электромагнитный момент якоря на колесе превысит момент силы тяги колеса?
15. Какие меры следует предпринять, если электродвигатели локомотива не в состоянии развить заложенную в проекте мощность?
16. Какие меры следует предпринять, чтобы увеличить расстояние между тяговыми подстанциями?
17. Почему наибольшее распространение имеет переменный ток? Тогда почему тяговые двигатели локомотивов постоянного тока?
15. ВЫСОКОСКОРОСТНОЙ ТРАНСПОРТ
1. Развитие наземного транспорта идет в направлении повышения безопасности движения и увеличения скорости движения. Повышение безопасности движения возможно при применении систем автоматического управления движением, созданием более безопасных локомотивов, вагонов и модернизации рельсового пути. Для увеличения скорости движения экипажей высокоскоростного наземного транспорта (ВСНТ) нужны новые физические подходы при создании силы тяги и уменьшении силы сопротивления движению.
При повышенной скорости движения возрастают, прежде всего, силы аэродинамического сопротивления. Аэродинамическая сила сопротивления пропорциональна квадрату скорости: 
. Плотность воздуха ρ понизить невозможно, за исключением движения экипажа в вакуумной трубе. Поэтому, во-первых, стали придавать поездам, скорость которых превышает 200 км/ч, обтекаемую форму как самолетам. Коэффициент аэродинамического сопротивления поезда в форме вытянутой капли Сх ≈ 0,1, меньше примерно в пять раз по сравнению с обычным поездом.
Во-вторых, следует устранить механический контакт между экипажем и рельсовым путем, устранив тем самым силу сопротивления при качении колес. Чтобы приподнять экипаж над дорожным полотном, можно применить воздушную подушку. Но, как показывает опыт, вентиляторы, нагнетающие воздух в зазор между днищем поезда и дорожным полотном, потребляют несопоставимое с выгодой количество энергии. Кроме того, они являются источником сильного шума и поднимают облака пыли. Рассматривается способ нагнетания встречного потока воздуха под днище аэропоезда или создание вакуума между полотном эстакады и крышей экипажа. Однако проектировщики ВСНТ останавливают свой выбор на системах электромагнитной и электродинамической подвески экипажа над дорожным полотном. Подъемная сила создается за счет взаимодействия магнитного поля экипажа с проводящей шиной дорожного полотна. Применение постоянных магнитов остается под вопросом, так как невозможно регулировать их подъемную силу.
В-третьих, необходимо создать достаточную для движения силу тяги. Колесо для этой цели мало пригодно, так как создает сопротивление движению. Кроме того, сила сцепления колеса с рельсом с увеличением скорости падает. Реактивные самолетные двигатели могут развить достаточную силу тяги. Но шум и вибрация превышает допустимые нормы. Поэтому проектировщики останавливают свой выбор на электромагнитном взаимодействии экипажа и токопроводящей шины дорожного полотна. Например, на экипаже устанавливается так называемый линейный асинхронный двигатель (ЛАД). Три или более обмотки двигателя расположены вдоль экипажа и при питании от трехфазной сети переменного тока создают бегущее назад магнитное поле. Поле взаимодействует с вихревыми токами в токопроводящей шине, отталкивает их от себя, а на экипаж действует такая же сила, направленная вперед.
2. Электромагнитный подвес основан на действии силы притяжения сердечника электромагнита, установленного на экипаже, с ферромагнитным рельсом дорожного полотна (рис. 15.1). Известно, что ферромагнитные материалы, например железо, намагничиваются и притягиваются в область наиболее сильного магнитного поля.
Подъемная сила электромагнита может быть определена по уравнению связи силы с потенциальной энергией. Сила равна первой производной от энергии по координате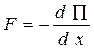 
. Установим зависимость потенциальной энергии взаимодействия электромагнита от расстояния х между феррорельсом и полюсными наконечниками (рис. 15.1). 
Как известно, энергия магнитного поля определяется формулами:
. (15.1)
Здесь J –– сила тока в катушке электромагнита, L –– индуктивность электромагнита, Ψ – потокосцепление катушки.
По закону Ома для магнитной цепи электромагнита, состоящей из сердечника электромагнита, феррорельса и двух воздушных зазоров, магнитные сопротивления которых включены последовательно, магнитный поток равен отношению магнитодвижущей силы JN к сумме магнитных сопротивлений:
. (15.2)
В этой формуле магнитные сопротивления магнитопровода и феррорельса объединены и l –– средняя длина силовых линий магнитного поля (пунктир на рис 15.1). Относительная магнитная проницаемость ферромагнитных материалов достигает десятков тысяч единиц, поэтому основной вклад в магнитное сопротивление дает воздушный зазор, относительная магнитная проницаемость которого равна единице. С увеличением воздушного зазора магнитный поток и энергия магнитного поля очень быстро уменьшаются.
Определим силу притяжения якоря к полюсам электромагнита как первую производную по расстоянию х между якорем и полюсами от энергии магнитного поля (15.1): 
.
. (15.3)
Сила притяжения пропорциональна квадрату индукции В магнитного поля в магнитопроводе электромагнита и быстро падает с увеличением ширины зазора. Наибольшая величина силы притяжения будет при зазоре х, равном нулю. Например, при массе экипажа 10 т даже при минимальном зазоре, когда электромагниты создают поле с индукцией 1 Тл, площадь сечения магнитопроводов электромагнитов должна быть 0,12 м2. Это обуславливает слишком большую массу электромагнитов. Выход может быть найден в применении сверхпроводящих магнитов с величиной индукции магнитного поля 3–4 Тл. Но это усложнит конструкцию экипажа из-за расположения криогенной установки на экипаже для охлаждения обмоток электромагнитов.
При движении экипажа необходимо достаточно точно поддерживать определенное значение ширины зазора между полюсами электромагнита и феррорельсом, при котором сила тяжести экипажа точно скомпенсирована силой притяжения. Стоит зазору увеличиться, как экипаж днищем упадет на полотно дороги, а стоит зазору уменьшиться, как электромагниты притянутся и прилипнут к феррорельсу. Подвешивание, основанное на притяжении, оказывается неустойчивым. Нужна быстродействующая автоматика регулирования силы тока в обмотках электродвигателя для поддержания экипажа на определенной высоте подвеса. Либо применить систему электродинамического подвеса, в которой возникают силы отталкивания электромагнитов и путевой шины.
3. Линейный асинхронный двигатель (ЛАД) предназначен для создания силы тяги экипажа ВСНТ при взаимодействии бегущего магнитного поля статора с токопроводящей путевой шиной. Статор двигателя представляет собой систему из трех, шести или более электромагнитов возбуждения поля, расположенных вдоль экипажа под его дном (рис.15.3). В этом случае шина устанавливается на дорожном полотне. Возможно обратное расположение: шина устанавливается на экипаже, а на полотне дороги устанавливается большое количество катушек возбуждения, включаемых в момент прохождения над ними экипажа.
 |
Катушки возбуждения подключены к сети трехфазного переменного напряжения. Максимум индукции магнитного поля создается сначала одной катушкой, в которой сила тока максимальная, а в соседних сила тока меньше из-за сдвига фаз, потом следующей и так далее. Таким образом, создается бегущее от головы экипажа к его хвосту магнитное поле. В режиме тяги скорость бегущего назад магнитного поля должна превышать скорость экипажа на величину скорости скольжения. При торможении – наоборот.
Когда магнитное поле со скоростью скольжения перемещается относительно путевой шины назад, в ней возбуждаются, вследствие явления электромагнитной индукции, вихревые индукционные токи. По правилу Ленца вихревые токи текут так, чтобы противодействовать перемещению магнитного поля, и значит, действовать на экипаж с силой тяги. При предельной скорости экипажа, равной скорости бегущего назад магнитного поля, магнитное поле стало бы неподвижным относительно шины, скорость скольжения стала бы равна нулю, вихревые токи и сила тяги исчезнут.
Рассмотрим более детально образование силы тяги на примере распределения магнитного поля в виде одной длины волны, которая перемещается по шине со скоростью скольжения (рис. 15.3). На самом деле при большом числе магнитов создается несколько волн, потому что больше магнитов, тем слабее краевой эффект. Представим распределение магнитного поля тяговых электромагнитов в виде четырех участков c линиями раздела a b c d e. На первом участке (a–b) индукция магнитного поля возрастает, значит, вихревой ток будет на этом участке шины циркулировать по часовой стрелке. В этом случае магнитное поле вихревых токов будет направлено за чертеж, препятствуя нарастанию магнитного поля, согласно правилу Ленца. На втором участке шины (b–c) магнитный поток тяговых электромагнитов уменьшается. Вихревые токи на этом участке, противодействуя уменьшению магнитного потока, будут, согласно правилу буравчика, циркулировать против часовой стрелки. На линии раздела участков b и d вихревые токи текут в одном направлении и складываются. В других местах шины, например на линии с, вихревые токи вычитаются.
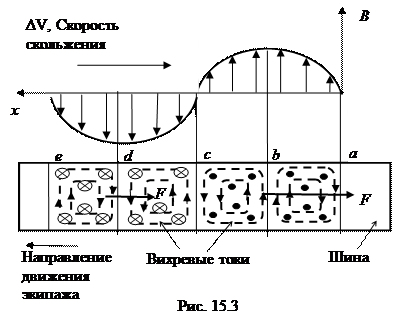Сила Ампера будет действовать на ту часть шины, где вихревые токи и индукция магнитного поля отличны от нуля, то есть на участки шины около линий раздела b и d. Сила Ампера, действующая на эти участки шины, по правилу левой руки будет направлена в сторону скорости скольжения, против направления движения экипажа. Согласно третьему закону Ньютона, на электромагниты экипажа будет действовать такая же сила тяги, направленная по ходу движения. Если скорость скольжения бегущего магнитного поля будет направлена в сторону движения экипажа, то будет происходить торможение экипажа.
Оценим приближенно силу тяги линейного асинхронного двигателя. Пусть индукция магнитного поля распределена вдоль шины по закону
. (15.4)
Здесь х =Δ V t –– координата участка шины от головы волны, λ – длина волны магнитного поля. Она равна расстоянию между первым и седьмым электромагнитом, у которых фазы силы тока отличаются на 2π.
ЭДС электромагнитной индукции, согласно закону Фарадея, равна скорости изменения магнитного потока сквозь поверхность контура: 
. Заменим сплошную шину отдельными воображаемыми контурами в виде рамок, по которым циркулируют вихревые токи. На рис. 15.3 это участок между линиями b–d, в котором ток циркулирует против часовой стрелки. Ширина рамки равна ширине шины b, а длина равна половине длины волны магнитного поля. Площадь рамки равна 
. ЭДС электромагнитной индукции в рамке, по закону Фарадея, равна 
. Дифференцируя уравнение магнитной индукции (15.4), получим
