Цель работы: изучить переходные процессы в цепи с индуктивностью при включении и выключении источника постоянного тока, измерить время релаксации и индуктивность катушки.
Оборудование: генератор, плата с катушкой и резисторами, осциллограф.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Переходный процесс – это процесс установления силы тока в электрической цепи при подключении к источнику напряжения или процесс спада силы тока до нуля при выключении. Если бы цепь состояла из проводника, обладающего только активным сопротивлением, то сила тока мгновенно достигла бы предельного значения 
, а при выключении мгновенно падала бы до нуля. Но таких цепей не бывает. Даже кусочек провода обладает и ёмкостью и индуктивностью, поэтому некоторое время происходят переходные процессы установления тока и напряжения.
Электрический ток J, текущий в контуре, создает магнитное поле. Магнитный поток, пронизывающий контур, прямо пропорционален силе тока: Ф = LJ. Коэффициент L называется индуктивностью контура. При всяком изменении силы тока магнитный поток изменяется. Это приводит согласно закону Фарадея к возникновению ЭДС самоиндукции, которая пропорциональна скорости изменения силы тока в самом контуре:
. (1)
Знак минус обусловлен правилом Ленца: ток самоиндукции направлен так, чтобы препятствовать изменению силы тока в контуре.
Индуктивность зависит от формы и размеров контура. Для увеличения индуктивности применяют катушки. Витки катушки можно рассматривать как последовательно соединенные контуры. Поэтому ЭДС самоиндукции катушки равна скорости изменения суммы магнитных потоков(Ψ= Σ Ф), называемых потокосцеплением. Для неферромагнитных сердечников ЭДС самоиндукции пропорциональна скорости изменения силы тока: 
.
Например, для катушки, называемой соленоидом, длина которой много больше диаметра, можно теоретически получить формулу индуктивности. Индукция магнитного поля соленоида определяется формулой 
. Тогда потокосцепление будет равно 
, откуда индуктивность равна L = μμ0n2V. Здесь μ – относительная магнитная проницаемость сердечника; μ 0 = 4π ∙10-7 Гн/м – магнитная постоянная; 
– число витков на единицу длины l; 
– объем сердечника.
Индуктивность катушки можно определить экспериментально, изучая процессы включения и выключения источника постоянного тока к катушке. По закону Ома, при включении источника падение напряжения на сопротивлении проводников цепи равно алгебраической сумме напряжения источника U и ЭДС самоиндукции: 
. При отключении в цепи действует только ЭДС самоиндукции 
. Это дифференциальные уравнения первого порядка. Разделив переменные и интегрируя, получим для включения и выключения цепи
; (2) 
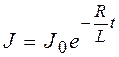. (3)
При включении сила тока нарастает, а при выключении источника спадает по экспоненциальному закону (рис. 1). Чем больше индуктивность цепи, тем дольше по времени происходят процессы установления и спада силы тока. Параметром переходного процесса является время релаксации τ. Это время, при котором показатель экспоненты становится равен единице 
. В течение этого времени сила тока при выключении спадает в е =2,72 раз, а при включении достигает 
. Формально предельная сила тока J 0 устанавливается через бесконечное время и по закону Ома равна 
.
В момент размыкания цепи ток прекращается не сразу, а продолжает течь через зазор ключа. ЭДС самоиндукции в начальный момент может быть велика, превышая напряжение источника во много раз 
. Это приводит к пробою зазора ключа с образованием искры или даже дугового разряда.
 |
Экспериментально определить индуктивность электрической цепи можно с помощью осциллографа по времени релаксации, если на экране получить осциллограммы силы тока при включении или выключении источника напряжения. Для этого в лабораторной установке к генератору прямоугольных импульсов подключается плата, в которой собирается цепь из катушки и резистора (рис.2). Сила тока в цепи пропорциональна напряжению на резисторе, которое измеряется осциллографом.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Подсоединить на плате проводниками одну из катушек индуктивности последовательно к одному из резисторов. Подсоединить к гнездам платы генератор и осциллограф.
2. Включить генератор и осциллограф в сеть 220 В. Выбрать кнопками на панели генератора режим прямоугольных импульсов и частоту несколько килогерц, ручку напряжения выхода Uвых поставить в среднее положение.
3. Переключателями осциллографа «Усиление» (Вольт/дел) и «Развертка» (мс/дел) и ручки синхронизации «Уровень» получить на экране устойчивое изображение, например, процесса спада силы тока во весь экран. Совместить начало линии процесса спада с левой вертикальной линией шкалы экрана, а почти горизонтальный участок конца процесса – с нижней горизонтальной линией шкалы (рис.3). Записать в табл. 1 параметры установки, коэффициент усиления и длительность развертки.
|
4. Измерить координаты X и Y точек осциллограммы в делениях шкалы не менее пяти раз по всей длине (рис. 3). Результаты записать в табл. 2.
Выключить приборы.
5. Определить время моментов измерения t = КхX. Определить силу тока в моменты измерения: 
. Записать в табл. 2.
6. Определить натуральные логарифмы силы тока. Результаты записать в табл. 2.
Таблица 1 Таблица 2
| X, дел | Y, дел | J, А | t, с | ln, J |
| Индуктивность L, мГн | |
| Сопротивление R, Ом | |
| Коэф фициент КY, мВ/дел | |
| Развертка КX, мс/дел | |
| Время релаксации <τ>, мс |
7. Построить график зависимости логарифма силы тока ln J от времени t. Если прологарифмировать уравнение (3), то получим уравнение линейной зависимости 
, где – время релаксации. Значит, около точек на графике следует провести прямую линию. Угловой коэффициент линии равен величине, обратной времени релаксации.
8. Построить на экспериментальной линии как на гипотенузе треугольник (рис. 4). Определить по графику среднее значение времени релаксации
. (6)
Результат записать в табл. 1.
9. Определить среднее экспериментальное значение индуктивности по времени релаксации <L>= <τ> R.
10. Оценить случайную погрешность измерения индуктивности по формуле
. (13)
Здесь n – число измерений.
11. Записать результат в виде L=<L> ± δL, Р = 0,90. Сравнить измеренное значение индуктивности с записанным значением на плате.
Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Объясните явление самоиндукции. Как направлены токи самоиндукции согласно правилу Ленца при включении и выключении источника тока?
2. Объясните роль индуктивности в электрической цепи. Почему катушки обладают большей индуктивностью, чем контур?
3. Выведите формулу для индуктивности соленоида. От чего зависит индуктивность катушек?
4. Выведите уравнение для силы тока в цепи при включении источника напряжения. Дайте определение времени релаксации.
5. Выведите уравнение для силы тока в цепи при выключении источника напряжения.
6. Объясните графический метод определения времени релаксации.
Работа 26 а
