Цель работы: изучить процесс электрических колебаний в колебательном контуре, определить параметры затухания и зависимость амплитуды вынужденных колебаний от частоты.
Оборудование: плата с колебательным контуром, генератор, осциллограф.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Собственные электрические колебания силы тока, напряжения, заряда возможны в электрической цепи, называемой колебательным контуром. Колебательный контур состоит из конденсатора C, катушки индуктивности L и резистора R, так как соединительные провода и провод катушки обладают сопротивлением (рис. 1).
 Если заряженный конденсатор замкнуть на катушку, то в цепи потечет ток. Cила тока возрастает постепенно, так как этому препятствует ЭДС самоиндукции катушки. В момент, когда конденсатор разрядится, ток не прекращается. Спаду силы тока снова препятствует ЭДС самоиндукции, и ток, продолжая течь в том же направлении, перезаряжает конденсатор. Затем процесс повторяется в обратном направлении.
Если заряженный конденсатор замкнуть на катушку, то в цепи потечет ток. Cила тока возрастает постепенно, так как этому препятствует ЭДС самоиндукции катушки. В момент, когда конденсатор разрядится, ток не прекращается. Спаду силы тока снова препятствует ЭДС самоиндукции, и ток, продолжая течь в том же направлении, перезаряжает конденсатор. Затем процесс повторяется в обратном направлении.
Затухающие колебания. В реальном контуре колебания будут затухающими. Уравнение для затухающих колебаний силы тока в контуре можно получить, решив уравнение закона Ома: сумма падений напряжений на конденсаторе и резисторе должна быть равна ЭДС самоиндукции: UC + J R = E. Переходя к одной переменной – к заряду 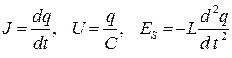 , получим дифференциальное уравнение
, получим дифференциальное уравнение
 . (1)
. (1)
Решением этого уравнения является функция зависимости заряда конденсатора от времени  , где q 0 – амплитуда заряда,
, где q 0 – амплитуда заряда,  – циклическая частота затухающих колебаний,
– циклическая частота затухающих колебаний,  – коэффициент затухания.
– коэффициент затухания.
Выражение  имеет смысл амплитуды заряда. Амплитуда при затухающих колебаниях со временем уменьшается по экспоненциальному закону (рис.2). Степень затухания колебаний характеризуется несколькими параметрами.
имеет смысл амплитуды заряда. Амплитуда при затухающих колебаниях со временем уменьшается по экспоненциальному закону (рис.2). Степень затухания колебаний характеризуется несколькими параметрами.
Во-первых, коэффициент затухания b. Если ввести время релаксации  , время, в течение которого амплитуда уменьшается в е = 2,72 раз, то е -bt = е – 1, b = 1 /t. Коэффициент затухания численно равен величине, обратной времени релаксации.
, время, в течение которого амплитуда уменьшается в е = 2,72 раз, то е -bt = е – 1, b = 1 /t. Коэффициент затухания численно равен величине, обратной времени релаксации.
Во-вторых, логарифмический декремент, характеризующий затухание колебаний в зависимости от числа совершенных колебаний. По определению он равен логарифму отношения амплитуд двух соседних колебаний:  . Если подставить сюда формулы для амплитуды, то получим связь между параметрами затухания
. Если подставить сюда формулы для амплитуды, то получим связь между параметрами затухания 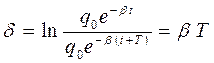 . Тогда уравнение для амплитуды можно записать через число колебаний
. Тогда уравнение для амплитуды можно записать через число колебаний
 . (2)
. (2)
 |
Экспериментальное измерение параметров затухания в колебательном контуре можно произвести по осциллограмме затухающих колебаний. Для этого контур подключается к генератору прямоугольных импульсов и осциллографу (рис. 3). В момент смены полярности напряжения конденсатора в контуре начинается колебательный разряд, наблюдаемый на экране осциллографа.
Вынужденные колебания. Чтобы электрические колебания были незатухающими, в колебательный контур следует включить источник переменного напряжения, например, как на рис. 3. При этом в уравнение закона Ома (1) следует добавить ЭДС источника:
 (3)
(3)
После включения источника в контуре возникают два вида колебаний: собственные и вынужденные колебания. Собственные колебания со временем затухают и остаются только вынужденные колебания. Поэтому решение уравнения (3) будем искать в виде функции для силы тока в виде J =J 0cos wt. Подставив в (3) соотношения:  ,
,  ,
, 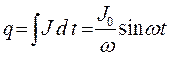 , получим
, получим
 . (4)
. (4)
 Для решения воспользуемся геометрическим методом векторных диаграмм. Проведем из полюса векторы, длины которых равны амплитудам членов уравнения (4) (рис. 4). Если эти векторы поворачивать с угловой скоростью, равной циклической частоте, то проекции векторов на ось напряжений будут равны членам уравнения (4). По теореме Пифагора для заштрихованного треугольника
Для решения воспользуемся геометрическим методом векторных диаграмм. Проведем из полюса векторы, длины которых равны амплитудам членов уравнения (4) (рис. 4). Если эти векторы поворачивать с угловой скоростью, равной циклической частоте, то проекции векторов на ось напряжений будут равны членам уравнения (4). По теореме Пифагора для заштрихованного треугольника  , откуда амплитуда силы тока равна
, откуда амплитуда силы тока равна
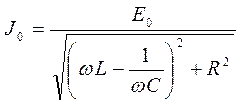 .(5)
.(5)
Это закон Ома для цепи переменного тока. Знаменатель следует трактовать как полное электрическое сопротивление цепи переменному току. Оно имеет три составляющих. Активное сопротивление R обусловлено сопротивлением движению электронов в кристаллической решетке проводника. Ограничение силы тока действием ЭДС самоиндукции эквивалентно индуктивному сопротивлению ωL. Емкостное сопротивление 1/(ωС) обусловлено ограничением тока процессами перезарядки конденсатора.
 Амплитуда силы тока согласно (5) зависит не только от ЭДС источника тока, но и от его частоты. С ростом частоты сила тока сначала возрастает, достигает максимума при частоте, близкой к частоте свободных колебаний, а потом уменьшается (рис. 5). Явление сильного возрастания амплитуды вынужденных колебаний при некоторой частоте называется резонансом. При резонансе напряжений падения напряжения на катушке индуктивности и на конденсаторе находятся в противофазе, равны друг другу и компенсируются. Сопротивление цепи равно только активному сопротивлению R. Поэтому сила тока при резонансе может достигать огромных значений J max = E 0 /R. Напряжения на конденсаторе и катушке могут во много раз превышать ЭДС источника.
Амплитуда силы тока согласно (5) зависит не только от ЭДС источника тока, но и от его частоты. С ростом частоты сила тока сначала возрастает, достигает максимума при частоте, близкой к частоте свободных колебаний, а потом уменьшается (рис. 5). Явление сильного возрастания амплитуды вынужденных колебаний при некоторой частоте называется резонансом. При резонансе напряжений падения напряжения на катушке индуктивности и на конденсаторе находятся в противофазе, равны друг другу и компенсируются. Сопротивление цепи равно только активному сопротивлению R. Поэтому сила тока при резонансе может достигать огромных значений J max = E 0 /R. Напряжения на конденсаторе и катушке могут во много раз превышать ЭДС источника.
По резонансной кривой можно определить параметры затухания контура. Если провести на уровне с ординатой  горизонтальную линию (рис. 5), то полуширина резонансной кривой будет равна коэффициенту затухания b = D w/ 2.
горизонтальную линию (рис. 5), то полуширина резонансной кривой будет равна коэффициенту затухания b = D w/ 2.
ВЫПОЛНЕНИЕ РАБОТЫ
Изучение затухающих колебаний.
1. Подсоединить к плате с колебательным контуром генератор и осциллограф. Выбрать, переключая проводники на плате, емкость и сопротивление контура.
2. Включить приборы в сеть 220 В. Выбрать кнопками на генераторе режим: импульсы прямоугольной формы, частота несколько килогерц. Переключателями осциллографа «Развертка» (доли мс/дел.) и «Вольт/дел» и ручкой синхронизации «Уровень» получить устойчивую осциллограмму одного колебательного разряда во весь экран. Записать параметры установки в табл. 1.
3. Определить амплитуды не менее пяти соседних колебаний с помощью масштабной сетки на экране осциллографа. Результаты измерений и параметры установки записать в табл. 2.
Таблица 1 Таблица 2
| Индуктивность L, мГн | 0,76 |
| Сопротивление R, Ом | |
| Емкость С, мкФ | |
| Частота ν, Гц |
| n | |||||
| А, дел | |||||
| ln A |
4.
4. Произвести расчеты. Определить значения натуральных логарифмов амплитуд.
5. Построить график зависимости логарифма амплитуды от числа совершенных колебаний. Размер графика не менее половины страницы. Если прологарифмировать уравнение (2), то получим линейную зависимость ln А = ln A 0 – d n, поэтому около точек следует провести прямую линию. Отклонения точек должны быть минимальны.
 6. Определить логарифмический декремент колебаний. Он равен угловому коэффициенту экспериментальной линии. Для этого на прямой как на гипотенузе построить прямоугольный треугольник. Среднее значение логарифмического декремента равно отношению катетов:
6. Определить логарифмический декремент колебаний. Он равен угловому коэффициенту экспериментальной линии. Для этого на прямой как на гипотенузе построить прямоугольный треугольник. Среднее значение логарифмического декремента равно отношению катетов:
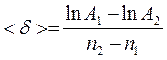 . (6)
. (6)
Определить среднее значение коэффициента затухания  . Сравнить с теоретическим значением
. Сравнить с теоретическим значением  .
.
Изучение вынужденных колебаний
1. Установить на генераторе режим синусоидальных колебаний, частоту, близкую к частоте собственных колебаний контура (десятки килогерц). На экране осциллографа должна наблюдаться развертка синусоидальных колебаний. Изменяя частоту генератора, убедиться, что при некоторой частоте амплитуда сильно возрастает.
2. Измерить амплитуду колебаний не менее десяти раз по шкале экрана в интервале частот 20 – 100 кГц. Вблизи резонанса измерения производить чаще. Результаты записать в табл. 3.
Выключить приборы. Таблица 3
| Частота nген, Гц | |||||||||
| Амплитуда А, дел |
3. Построить график зависимости амплитуды от частоты. Размер графика не менее половины страницы. Указать равномерный масштаб. Около точек провести плавную линию.
4. Определить по графику резонансную частоту и амплитуду при резонансе А max. Вычислить 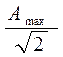 . Провести на графике линию с этой ординатой. Определить абсциссы точек пересечения с резонансной кривой. Найти по графику полуширину резонанса (рис. 5).
. Провести на графике линию с этой ординатой. Определить абсциссы точек пересечения с резонансной кривой. Найти по графику полуширину резонанса (рис. 5).
5. Определить коэффициент затухания  . Сравнить результат с теоретическим значением и с результатом расчета для затухающих колебаний. Сделать выводы.
. Сравнить результат с теоретическим значением и с результатом расчета для затухающих колебаний. Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Объясните, почему в контуре возможны собственные электрические колебания.
2. Запишите уравнение закона Ома для колебательного контура. Запишите решение уравнения для затухающих колебаний. Изобразите график затухающих колебаний.
3. Дайте определение коэффициента затухания, логарифмического декремента. Каков их физический смысл?
4. Запишите уравнение закона Ома для вынужденных колебаний. В каком виде находится его решение для силы тока?
5. Дайте определение резонанса. Чем опасен резонанс?
6. Объясните способ определения коэффициента затухания по резонансной кривой. Докажите, что коэффициент затухания равен полуширине резонансной кривой.
Работа 24 б






