|
|
В результате диффузии электронов и дырок полупроводник типа — n приобретает положительный потенциал. Электроны этого полупроводника получат дополнительную, отрицательную энергию 
(заряд электрона отрицателен). Энергетические уровни полупроводника типа — n опускаются. Полупроводник типа — p приобретает отрицательный потенциал. Электроны этого полупроводника получают дополнительную положительную энергию и его энергетические уровни поднимаются. Этот процесс будет происходить до тех пор, пока не станут одинаковыми уровни Ферми обоих кристаллов.
В состоянии равновесия на границе p - n число переходов электронов слева направо равно числу переходов справа налево. Справа электронов много, но им надо преодолеть потенциальный барьер D W (вероятность перехода пропорциональна 
). Слева электронов мало, зато они свободно спускаются с потенциального барьера. В результате незначительные электронные токи справа и слева равны. Это же можно сказать и о дырочных токах.
Приложим теперь к p-n переходу внешнюю разность потенциалов U так, чтобы на p — полупроводник подавался положительный потенциал, а на n — полупроводник отрицательный, т. е. внешнее поле направлено против контактного поля p-n перехода. Энергетические уровни n-полупроводника поднимутся, а p-полупроводника опустятся. Потенциальный барьер D W уменьшится на 
. Уменьшение потенциального барьера приведет к резкому увеличению потока электронов справа налево и дырок слева направо. Равновесие нарушается. Через p-n переход пойдет ток тем более сильный, чем больше U.
При подключении источника тока в обратном направлении (плюс на n– полупроводник, и минус на p– полупроводник), внешнее поле, по направлению, совпадает с контактным полем p–n перехода. Потенциальный барьер D W возрастает, и поток электронов из n в p практически исчезает, а из p в n остается, практически, таким же, что и был в равновесии, очень слабым. Идет слабый ток, создаваемый только не основными носителями тока полупроводников p и n.
___________________________________________________________________
Для решения задач электростатики в неоднородной среде удобно ввести вспомогательную величину — вектор электрического смещения 
.
.
|
Целесообразность введения этой величины можно пояснить следующим примером. На рис. Изображена граница раздела двух сред. Пусть линии вектора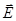 
перпендикулярны границе раздела и 
. Поэтому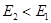 
, что отмечено на рисунке густотой силовых линий. 
; 
; 
, т.е.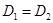 
.
Это значит, что величина не изменяется при переходе границы, в то время как величина 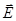меняется скачкообразно.
Линии вектора проводятся и определяются так же, как и линии вектора 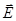. Величина 
называется потоком вектора .
Запишем теорему Гаусса для напряженности электрического поля 
. В среде напряженность в каждой точке уменьшится в e раз, а следовательно и поток вектора напряженности будет уменьшен в e раз. Умножая левую и правую части равенства теоремы Гаусса на ee 0, получим теорему Гаусса для потока вектора
, 
.
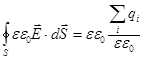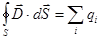Из последнего равенства видно, что [ФD] = Кл, а [D] = Кл/м 2.
