Прохождение тока через проводник, обладающий сопротивлением, всегда сопровождается выделением теплоты. Количество теплоты, выделившегося за время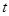 
определяется законом Джоуля — Ленца:
.
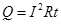Это соотношение было установлено экспериментально Джоулем и независимо от него Ленцем для однородного участка цепи, однако оно будет справедливо и для неоднородного участка при условии, что действующие в нем сторонние силы имеют нехимическое происхождение. Если сила тока изменяется со временем, то количество теплоты, выделяющееся за время 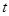, вычисляется по формуле
Выразим закон Джоуля — Ленца в дифференциальной форме (для физической точке токопроводящей среды). Для этого введем понятие удельной тепловой мощности тока. Под удельной тепловой мощностью тока 
подразумевается величина, измеряемая количеством теплоты, выделяемой в единицу времени в единице объема проводника, т. е. равна тепловой мощности выделяемой в единице объема 
, и измеряется в ваттах на кубический метр 
. Согласно закону Джоуля — Ленца тепловая мощность 
.
Выделим в проводнике элементарный объем в виде цилиндра длиной 
и площадью основания 
. В объеме 
этого цилиндра выделяется тепловая мощность 
, где 
— сила тока, протекающего через площадь основания , 
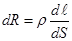— сопротивление, выделенного цилиндра. А, удельная тепловая мощность будет равна 
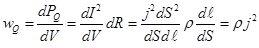. Учитывая что 
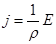, запишем
.
Эта запись и выражает закон Джоуля — Ленца в дифференциальной форме.
