Энергию заряженного конденсатора можно выразить через величину, характеризующую электрическое поле — через напряженность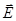 
. Убедимся в этом сначала на простейшем примере плоского конденсатора. Подстановка в формулу 
выражения 
дает 
. Умножив и числитель и знаменатель правой части этого равенства на d, получим 
. А поскольку 
и 
(объем между обкладками конденсатора), то
.
Эта формула подводит к физической идее о локализации энергии в самом поле. Данное предположение нашло опытное подтверждение в области переменных во времени полей. Электромагнитные волны переносят энергию, — уже это заставляет нас признать, что носителем энергии является само поле.
Полученная формула справедлива для однородного поля конденсатора, заполняющего объем 
. Из нее следует, что электрическая энергия распределена в пространстве с объемной плотностью 
.
В более строгом курсе физики доказывается, что формула объемной плотности энергии справедлива не только для однородного поля, но и для любого не однородного поля, изменяющегося во времени 
. Тогда энергию неоднородного поля можно найти интегрированием
по объему, занимаемым полем.
