Свободные заряды в однородном проводнике располагаются на его поверхности. Это является следствием отталкивания одноименных точечных зарядов, сила взаимодействия которых, убывает точно обратно пропорционально квадрату расстояния между ними, а не по другому закону. При равномерном распределении заряды внутри проводника отсутствуют. Применяя теорему Гаусса к произвольной замкнутой поверхности внутри проводника, убедимся, что в этом случае электрическое поле внутри проводника также отсутствует 
. Из равенства нулю напряженности поля 
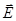следует, что во всех точках проводника потенциал имеет одно и то же значение. Одинаковое во всех точках проводника значение потенциала называется потенциалом проводника.
|
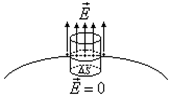
Линии поля 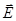заряженного проводника исходят перпендикулярно к поверхности этого проводника. Выберем в качестве замкнутой поверхности небольшой цилиндр (как показано на рисунке). Тогда поток вектора 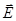через эту поверхность будет равен только потоку через «наружный» торец цилиндра (потоки через боковую поверхность и внутренний торец равны нулю).По теореме Гаусса мы имеем 
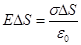. Сократив обе части этого равенства на 
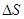получим
.
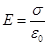Из формулы видно, что напряженность результирующего поля вблизи поверхности проводника связана только с плотностью зарядов на его поверхности. Выразим поверхностную плотность заряда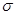 
через потенциал заряженного проводника 
. В частности, для проводящего шара потенциал в центре, а, следовательно, и для любой его точки равен 
, где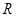 
— радиус шара. Учитывая, что 
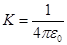запишем, 
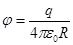. Выразив, заряд 
через потенциал
,
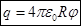определим поверхностную плотность заряда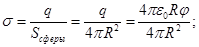 
.
При заданном потенциале поверхностная плотность заряда 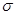обратно пропорциональна радиусу шара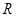
.
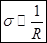Этот результат имеет общий характер, какой бы сложной формой ни обладало проводящее тело. Поверхностная плотность заряда будет больше в тех местах, где меньше R, т. е., где поверхность искривлена сильнее. Очевидно, что в этих же местах будет большей и напряженность электрического поля.
