Поле точечного заряда является центральным, а, следовательно, и потенциальным. В потенциальном поле работа по перемещению заряда не зависит от выбора траектории движения, а зависит лишь от начального и конечного положений заряда в этом поле. В этом случае работа по перемещению заряда по замкнутой траектории будет равна нулю. Математически это можно выразить в виде 
. Учитывая, что 
, получим 
. После сокращения на величину заряда 
, запишем условие потенциальности электростатического поля
.
Циркуляция напряженности электрического поля равна нулю (в математике линейный интеграл по замкнутой траектории называют циркуляцией).
В каждой точке поля заряд обладает значением потенциальной энергии, а работа сил поля по перемещению заряда равна уменьшению потенциальной энергии 
.
Для бесконечно малого перемещения 
, или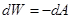 
. Интегрируя, определим потенциальную энергию заряда в поле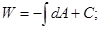 
. Постоянная интегрирования 
зависит от выбора точки поля, в которой потенциальная энергия условно считается равной нулю.
Разные пробные заряды будут обладать в одной и той же точке поля различной энергией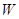 
. Однако отношение 
будет для всех зарядов одним и тем же.
Величина 
называется потенциалом поля в данной точке. Из определения следует, что потенциал численно равен потенциальной энергии, которой обладал бы в данной точке поля положительный единичный заряд.
Так для поля точечного заряда потенциальная энергия пробного заряда (потенциальная энергия системы двух точечных зарядов) будет равна 
. Будем считать, что в бесконечно удаленной точке (
) потенциальная энергия обращается в нуль, тогда 
, и
.
Учитывая потенциальную энергию пробного заряда в поле точечного заряда, получим формулу потенциала поля точечного заряда
