Найдем взаимосвязь между напряженностью Е электростатического поля, являющейся его силовой характеристикой, и потенциалом φ – энергетической характеристикой поля.
Работа по перемещению точечного, положительного заряда q вдоль произвольного направления х из точки 1 в бесконечно близкую к ней точку 2, х 2 – х 1 = d х, будет равна: А1,2 = q· Е х ∙d х или через потенциал: А1,2 = q(φ1 – φ2) = - q ·dφ. Откуда:
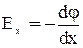, (12)
т.е. напряженность поля равна градиенту потенциала, взятому со знаком минус. Это означает, что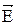 
направлен в сторону убывания потенциала.
Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхность, во всех точках которой потенциал φ имеет одно и то же значение. Для точечных зарядов в однородной среде, например, эти поверхности представляют собой сферы (рис.133а Трофимова, стр139).
Для любой точки поля линии напряженности всегда направлены по нормали к эквипотенциальным поверхностям. (рис.133б Трофимова, стр139).
