Уравнения состояния реальных газов

Для определения многих физических св-в прир. газов исп-ся ур-ие состояния. Уров-ем состояния наз-ся арифмет-ая завис-ть между параметрами, описывающими поведение простого или сложного вещ-ва. В кач-ве таких пар-ов исп-ся P,V и Т. Для идеальных газов исп-ся след-ее ур-ие состояния Клайперона-Менделеева PV=MRT, где Р – давление, Па; V – объем, м3; М – масса газа,кг; Т – темп-ра, К; R – универсальная газовая постоянная, кДж/(кгК). Для описания поведения реальных газов в последнее вводят корректирующий множитель,называе6мый коэф-ом сверхсжимаемости z – PV=zMRT. Голландский физик Ван-дер-Вальс в 1879г. предложил учитывать собственный объем молекул газа и силы взаимного притятежения посредством введения дополнительных членов в уравнения К-М. (Р+а/V2)(V-b)=RT, где V – удельный объём газа; а/V2 – константа сцепления молекул; b – поправка на объём молекул. Это уравнения состояние удовлетворительно описывает поведение реальных газов лишь при давлениях до 10 МПа и температурах 283-293 К, но оно не может численно описывать поведение природных УВ-ых газов гомологического ряда метана. Дальнейший процесс науки и техники требовал разработки более точного уравнения состояния природных газов, способного правильно описывать поведение их при давлениях до 100 МПа и тем-рах до 573 К в процессах добычи газа и при давлениях до 20 МПа и низких тем-рах до 123-93 К в процессах переработки прир. газов. В решении этой проблемы выявилось два направления: 1) введение коэф. Z в ур-ие сост. идеал. газа учитывающего отклонение реального газа от идеального; 2) добавление в ур-ие сост. идеал. газа большого числа констант. Так появились уравнения состояния:

1) Редлиха-Квонга: 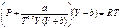, где ,

2) Пенга-Робинсона: ,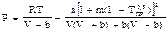

где , .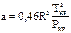

Тпр=Т/Ткр; m=0,37+1,54ω-0,27ω², ω – ацентрический фактор, учитывающий нецентральность сил взаимодействия м/у сложными молекулами

3) Бритти-Бриджмена (5 констант)

4) Бенедикта-Вебба-Рубина (8 пробел констант)

и т.д.