Игры, имеющие и не имеющие седловые точки

Если в игре с матрицей А α =β, то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры

 = α = β.

Седловая точка – это пара чистых стратегий (i_о,j_о) соответственно игроков 1 и 2, при которых достигается равенство α =β. В это понятие вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке. Математически это можно записать и иначе:

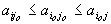
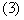
где i, j – любые чистые стратегии соответственно игроков 1 и 2; (i_о,j_о) – стратегии, образующие седловую точку.

Таким образом, исходя из (3), седловой элемент является минимальным в i_о-й строке и максимальным в j_о-м столбце в матрице А. Отыскание седловой точки матрицы А происходит следующим образом: в матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своём столбце. Если да, то он и есть седловой элемент, а пара стратегий, ему соответствующая, образует седловую точку. Пара чистых стратегий (i_о,j_о) игроков 1 и 2, образующая седловую точку и седловой элемент , называется решением игры. При этом i_о и j_о называются оптимальными чистыми стратегиями соответственно игроков 1 и 2.

Если седловой точки нет, то используется смешанная стратегия: А и В могут использовать все стратегии с некоторыми вероятностями.

Пример 1

Седловой точкой является пара (i_о = 3; j_о = 1), при которой  = = = 2.

Заметим, что хотя выигрыш в ситуации (3;3) также равен 2 = = , она не является седловой точкой, т.к. этот выигрыш не является максимальным среди выигрышей третьего столбца.

Пример 2

Из анализа матрицы выигрышей видно, что 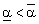, т.е. данная матрица не имеет седловой точки. Если игрок 1 выбирает свою чистую максиминную стратегию i = 2, то игрок 2, выбрав свою минимаксную j = 2, проиграет только 20. В этом случае игроку 1 выгодно выбрать стратегию i = 1, т.е. отклониться от своей чистой максиминной стратегии и выиграть 30. Тогда игроку 2 будет выгодно выбрать стратегию j = 1, т.е. отклониться от своей чистой минимаксной стратегии и проиграть 10. В свою очередь игрок 1 должен выбрать свою 2-ю стратегию, чтобы выиграть 40, а игрок 2 ответит выбором 2-й стратегии и т.д.

9.Сформулируйте свойства эластичности для ЛПФ.выпишетие выражение е₁,е₂,е_х

Эластичность - это отношение относительного прироста функции (зависимой переменной) к относительному приросту аргумента (независимой переменной).

Эластичностью переменной у по переменной х называется предел:

Е_х[f] = lim (y:y): (x:x)

x->0

1. Эластичность в х₀ суммы у = у1+…+уn положительных функций y_i = f_i(x)

i = 1…n удовлетворяет соотношению E_min ≤ E_y ≤ E_max

E_min и E_max – это мин/макс эластичности в х₀ функции у₀

2. Эластичность произведения функций u = u(x) и v = v(x) в точке равна сумме эластичности функций u и v в этой же точке: E_u*v = E_u + E_v

3. Эластичность частного функций u = u(x) и v = v(x) в точке равна разности эластичности функций u и v в этой же точке: E_u:v = E_u - E_v

4. Для функций y = f(x) и x = g(t) эластичность y по f в точке t₀: Eyt_(t0) = E_yx(g(t0))E_xt(t0)

5. Для функции y = f(x) эластичность обратной функции в точке y₀ удовлетворяет отношению: E_xy(y₀) = E^-1_yx(g(y₀))