Докажите принцип оптимальности Белмана

Сформулированный Р. Беллманом принцип оптимальности гласит: отрезок оптимального процесса от любой его точки до конца процесса сам является оптимальным процессом с началом в данной точке.

Изображена оптимальная траектория «Выберем производственный момент времени, 0<t₁<T

Предположим, что принцип оптимальности неверен. Тогда существует другой участок траектории, который будет оптимальным на последнем интервале (t1,T), тогда интеграл I в силу свойства аддитивности можно записать так:

1) На оптимальной траектории (I-II):I₁=

2) По (I-III): I₂ =

↓↓↓

I₂<I₁ - противоречие тому, что траектория I,II является оптимальной

Дайте определение оптимальности по Слейтеру.Приведите примеры.

Точка х_с Хназывается оптимальной по Слейтеру,если х_с 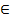Х х Х U(x)>U(x_c).В пространстве критериев U_c U U U,U>U_c.