Виноградова Татьяна, Н-2-2
Теоретическая часть. Методы оптимальных решений
Сформулируйте геометрическую интерпретацию игры 2х2
Решение игры 2×2 допускает наглядную геометрическую интерпретацию. Пусть игра задана платежной матрицей Р = (aij), i, j = 1, 2. По оси абсцисс (рис. 3.1) отложим единичный отрезок A1 A2 точка A1(х=0) изображает стратегию A1, а все промежуточные точки этого отрезка — смешанные стратегии SA первого игрока, причем расстояние от SA до правого конца отрезка — это вероятность p1 стратегии A1, расстояние до левого конца — вероятность p2 стратегии A2. На перпендикулярных осях I — I и II — II откладываем выигрыши при стратегиях A1 и A2 соответственно. Если 2 -й игрок примет стратегию B1, то она дает выигрыши a11 и a21 на осях I — I и II — II, соответствующие стратегиям A1 и A2. Обозначим эти точки на осях I—I и II—II буквой B1. Средний выигрыш v1, соответствующий смешанной стратегии SA, определяется по формуле математического ожидания v1 = a11 p1 + a21 p2 и равен ординате точки M1, которая лежит на отрезке B1 B1 и имеет абсциссу SA (рис. 3.1).

| 
|
| Рис. 3.1 | Рис. 3.2 |

Аналогично строим отрезок B2B2, соответствующий применению вторым игроком стратегии B2 (Рис. 3.2). При этом средний выигрыш v2 = a12 p1 + a22 p2 — ордината точки M2.
В соответствии с принципом минимакса оптимальная стратегия S*A такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум. Ординаты точек, лежащих на ломаной (рис. 3.3 в примере 3.4.1), показывают минимальный выигрыш игрока А при использовании им любой смешанной стратегии (на участке B1 N — против стратегии B1 , на участке NB2 — против стратегии B2). Оптимальную стратегию S*A = (p*1 , p*2) определяет точка N, в которой минимальный выигрыш достигает максимума; ее ордината равна цене игры v.
2.Как изменится оптимальное решение транспортной задачи при малом изменении потребностей или ресурсов?
Транспортная задача, в которой суммарные запасы

и суммарные потребности
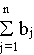
совпадают, называется закрытой моделью; в противном случае - открытой. Открытая модель решается приведением к закрытой.
В случае, когда суммарные запасы превышают суммарные
потребности, т.е.
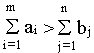
вводится фиктивный n+1 потребитель, потребности которого

В случае, когда суммарные потребности превышают суммарные
запасы, т.е.

, вводится фиктивный m+1 поставщик, запасы которого

Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика
полагают равными нулю, так как груз в обоих случаях не перевозится.






