Теория универсальности Фейгенбаума

На примере модели (14.2) можно проследить не только качественные, но и удивительные количественные закономерности. Для этого построим график По оси будем откладывать точки, принадлежащие устойчивым циклам. Так, циклу будет соответствовать одна устойчивая точка, циклу – две точки на одной вертикали, циклу - четыре и т. д. (см. рисунок).

Обозначим через значения параметра l, при которых происходят удвоения, а через - значения параметра, при которых х = 1/2 является элементом циклов Введём также величины d ₁, d ₂,..., равные расстоянию между х = 1/2 (элементом цикла 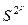при ) и ближайшем к нему элементом того же цикла. Расчёты, проведённые на ЭВМ, показали, что числа l и d обладают следующими свойствами:

Возьмём теперь вместо функции (14.2) любую другую симметричную функцию, которая имеет на отрезке [0,1] один максимум и около вершины близка к квадратичной параболе. Пусть в ней также происходит бесконечная последовательность бифуркаций удвоения при изменении некоторого параметра. Как показали исследования, для любой такой модели числа a и d будут одинаковыми.

Эти закономерности были обнаружены американским ученым М. Фейгенбаумом в 1978 г. В силу универсальности чисел a и d эту теорию называют теорией универсальности Фейгенбаума.

Теория Фейгенбаума приводит к парадоксальному выводу: между хаосом и порядком есть глубокая внутренняя связь. Непериодический, случайный процесс возникает как предел всё более усложняющихся структур (циклов 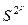). Хаос возникает как сверхсложная организация (цикл ). Этот вывод является общим, он может относиться к моделям экологии, гидродинамики, химическим моделям, т.е. к любым системам, где есть последовательность бифуркаций удвоения периода. В этом случае независимо от конкретного вида системы и её сложности теория даёт количественные предсказания; a и d выступают здесь как числа p и е.