Рассмотрим методику определения устойчивости неподвижных точек отображения (14.2).
Если значение 
находится в окрестности неподвижной точки 
справедливо равенство:
(14.5)
где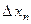 
- малая величина. Если точка 
устойчива, то с ростом номера последовательности n величина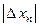 
должна уменьшаться. Запишем соотношение (14.2) с учётом (14.5) и разложим правую часть в ряд Тейлора:
Последнее приближённое равенство выполняется тем точнее, чем меньше 
С учётом (14.3) получим:
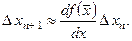
Следовательно, для того чтобы 
должно выполняться неравенство:
(14.6)
Это и есть условие устойчивости неподвижных точек отображения (14.2).
Определим, при каких значениях параметра l будут устойчивы неподвижные точки (14.4). Производная от функции f (x) отображения (14.2) равна:
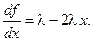
Для неподвижной точки 
имеем:
Следовательно, точка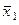 
действительно устойчива при l < 1.
Для неподвижной точки 
получаем:
Следовательно, точка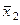 
будет устойчива для значений параметра
При l > 3 неподвижная точка 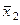теряет устойчивость.
