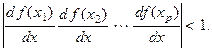Рассмотрим отображение:
(14.7)
График функции (14.7) пересекается с прямой у = х во всех неподвижных точках отображения (14.2):
а также в точках, принадлежащих циклу 
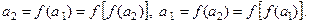
Увеличивая параметр l, мы растягиваем функцию 
вдоль оси у (см. рисунок). Если при некотором значении l линии у = х и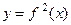 
пересекаются в одной точке, то с увеличением l могут появиться ещё две точки пересечения, которые и будут определять цикл 
Таким образом, переход 
в отображении f (x) обусловлен тем, что в отображении одна из неподвижных точек теряет устойчивость, и в её окрестности появляются две новые устойчивые неподвижные точки.
Следующие удвоения происходят аналогично. Их можно проследить, рассматривая функции 
и т. д.
Действуя так же, как при исследовании устойчивости неподвижных точек, можно показать, что устойчивость цикла с элементами 
будет определяться формулой:
