Бифуркация удвоения периода
Рассмотрим процесс роста бактерий в биореакторе (ферментёре). Если один раз за характерный период времени определять количество бактерий (х), мы получим последовательность, описывающую изменение численности бактерий:
Естественно ожидать, что численность популяции в данный момент времени зависит от того, сколько бактерий было в ферментёре в момент предыдущего замера. Математическая модель изменения численности популяции часто представляется в виде:
(14.1)
где l - коэффициент роста численности популяции; N - максимальное значение численности вида.
Из уравнения (14.1) видно, что численность популяции быстро растёт, пока она мала 
и начинает убывать, когда бактерий становится слишком много.
Если провести обезразмеривание модели (14.1) с помощью соотношений
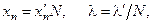
тогда она примет следующий вид (штрихи опущены):
(14.2)
Уравнения типа (14.2) называются логистическими.
