 Пусть функция
Пусть функция 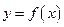 определена на отрезке
определена на отрезке  Произведем разбиение (см. Р5)
Произведем разбиение (см. Р5)


отрезка  на частичные отрезки
на частичные отрезки  и выберем произвольно точки
и выберем произвольно точки  Вычислим значения
Вычислим значения
 и составим так называемую интегральную сумму
и составим так называемую интегральную сумму

Определение 3. Если существует конечный предел интегральных сумм:

и если этот предел не зависит от вида разбиения  и выбора точек
и выбора точек  то его называют определенным интегралом отфункции
то его называют определенным интегралом отфункции 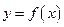 на отрезке
на отрезке  Обозначение:
Обозначение: 
 При этом саму функцию
При этом саму функцию 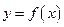 называют интегрируемой на отрезке
называют интегрируемой на отрезке 
(заметим, что число  называется диаметром разбиения
называется диаметром разбиения  ).
).
Пусть теперь функция  По разбиению
По разбиению  строится ступенчатая фигура (см. Р6), состоящая из прямоугольников
строится ступенчатая фигура (см. Р6), состоящая из прямоугольников  высоты
высоты  и длиной основания, равной
и длиной основания, равной  Площадь этой ступенчатой фигуры (достройте ее самостоятельно) равна интегральной сумме
Площадь этой ступенчатой фигуры (достройте ее самостоятельно) равна интегральной сумме  и эта площадь будет приближенно равна площади криволинейной трапеции[2]
и эта площадь будет приближенно равна площади криволинейной трапеции[2]  т.е.
т.е. 
 причем это равенство будет тем точнее, чем меньше диаметр разбиения
причем это равенство будет тем точнее, чем меньше диаметр разбиения  и оно становится точным при
и оно становится точным при 

Мы пришли к следующему геометрическому смыслу определенного интеграла:
интеграл  численно равен площади
численно равен площади  криволинейной трапеции
криволинейной трапеции  с верхней границей, описываемой уравнением
с верхней границей, описываемой уравнением 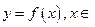

Замечание 3. В определении 3 интеграла  предполагается, что отрезок интегрирования ориентирован от
предполагается, что отрезок интегрирования ориентирован от  до
до  (т.е.
(т.е.  ). В случае противоположной ориентации отрезка
). В случае противоположной ориентации отрезка 
(т.е. при  ) полагаем по определению
) полагаем по определению  Также полагаем по определению, что
Также полагаем по определению, что 
Перейдем к формулировке свойств определенного интеграла.
Ограниченность подынтегральной функции. Если функция 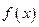 интегрируема на отрезке
интегрируема на отрезке  то она ограничена на этом отрезке (т.е.
то она ограничена на этом отрезке (т.е.  ).
).
Линейность интеграла. Если функции 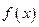 и
и 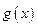 интегрируемы на отрезке
интегрируемы на отрезке  то на этом отрезке интегрируема и любая их линейная комбинация
то на этом отрезке интегрируема и любая их линейная комбинация  и имеет место равенство
и имеет место равенство 
Аддитивность интеграла. Если функция 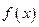 интегрируема на максимальном из отрезков
интегрируема на максимальном из отрезков 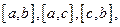 то она интегрируема и на двух других отрезках, причем имеет место равенство
то она интегрируема и на двух других отрезках, причем имеет место равенство 
Далее везде предполагаем, что 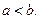
Монотонность интеграла. Если функции  и
и  интегрируемы на отрезке
интегрируемы на отрезке  и
и  то
то 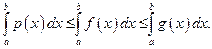
Интегрируемость модуля. Если функции 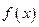 интегрируема на отрезке
интегрируема на отрезке  то на этом отрезке интегрируема и функция
то на этом отрезке интегрируема и функция 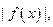 причем имеет место неравенство
причем имеет место неравенство
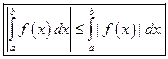
Теорема о среднем для интеграла. Пусть функция 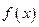 непрерывна на отрезке
непрерывна на отрезке  Тогда существует точка
Тогда существует точка  такая, что
такая, что  (геометрический смысл этой теоремы состоит в том, что существует прямоугольник с основанием
(геометрический смысл этой теоремы состоит в том, что существует прямоугольник с основанием  и высоты
и высоты  равновеликий криволинейной трапеции
равновеликий криволинейной трапеции  ).
).
Доказательство. Пусть  (по теореме Вейерштрасса значения
(по теореме Вейерштрасса значения 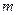 и
и  функцией
функцией 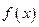 достигаются). Имеем
достигаются). Имеем  поэтому из свойства монотонности интеграла отсюда получаем
поэтому из свойства монотонности интеграла отсюда получаем

Последние неравенства показывают, что значение  является промежуточным для функции
является промежуточным для функции 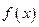 на отрезке
на отрезке  а, значит, по теореме Больцано-Коши существует
а, значит, по теореме Больцано-Коши существует  такое, что
такое, что

Теорема доказана.
Рассмотрим ещё несколько примеров, которые демонстрируют простейшие приемы интегрирования.


[1] Здесь и всюду далее с тем, чтобы не прерывать выкладки, в квадратных скобкахбудем указывать соответствующие замены переменных или формулы, необходимые для преобразований исходных выражений.
[2] На рис. Р6: – это трапеция ограниченная сверху кривой снизу– осью, с боков– прямыми и






